
分析 (1)f(x)=$\frac{a+lnx}{x}$的最大值为1,则函数f(x)在(0,+∞)不单调,故有极值点,继而到函数的最大值,求出a即可,
(2)分别根据导数和函数的最值的关系,求出p(x)和q(x)最值,即可证明.
解答 解:(1)∵f(x)=$\frac{a+lnx}{x}$,x>0,
∴f′(x)$\frac{1-a-lnx}{{x}^{2}}$,
∵函数f(x)=$\frac{a+lnx}{x}$的最大值为1
∴f′(x)$\frac{1-a-lnx}{{x}^{2}}$=0,解得x=e1-a,此时a≤1
∴f(x)max=f(e1-a)=$\frac{1}{{e}^{1-a}}$=1,
解得a=1
(2)由(1)可知q(x)=$\frac{f(x)}{e+1}$=$\frac{1+lnx}{x(e+1)}$,
∴q′(x)=$\frac{-lnx}{{x}^{2}}$<0在(1,+∞)恒成立,
∴q(x)在(1,+∞)为减函数,
∴q(x)<q(1)=$\frac{1}{e+1}$,
∵p(x)=$\frac{2{e}^{x-1}}{(x+1)(x{e}^{x}+1)}$,x>1,
∴p′(x)=2ex-1•$\frac{(-2x{e}^{x}+x)}{(x+1)^{2}(x{e}^{x}+1)^{2}}$>0在(1,+∞)恒成立,
∴p(x)在(1,+∞)为增函数,
∴p(x)>p(1)=$\frac{1}{e+1}$,
∴p(x)>q(x),
∴q(x)是p(x)的“线上函数”.
点评 本题考查导数的运用:求单调区间和极值、最值,考查新定义的理解和运用,注意运用构造函数法,以及恒成立问题的解法,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.
如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
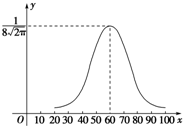 某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.
某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com