
【题目】如图,在四棱锥![]() 中,
中, ![]()
![]() 平面
平面![]() ,
,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
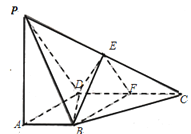
(Ⅰ)证明:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() .
.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与证明,往往从两个方面进行,一是从平几知识,如矩形得AB![]() BF,二是从立几知识,如从面面垂直出发,得线面垂直,再得线线垂直(Ⅱ)求二面角,一般利用空间向量进行求解,先根据题意确定空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据空间向量数量积求向量夹角,最后根据向量夹角与二面角之间关系求二面角
BF,二是从立几知识,如从面面垂直出发,得线面垂直,再得线线垂直(Ⅱ)求二面角,一般利用空间向量进行求解,先根据题意确定空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据空间向量数量积求向量夹角,最后根据向量夹角与二面角之间关系求二面角
试题解析:(Ⅰ)证:由已知DF∥AB且![]() DAB为直角,故ABFD是矩形,
DAB为直角,故ABFD是矩形,
从而AB![]() BF.
BF.
又PA![]() 底面ABCD, ∴平面PAD
底面ABCD, ∴平面PAD![]() 平面ABCD,
平面ABCD,
∵AB![]() AD,故AB
AD,故AB![]() 平面PAD,∴AB
平面PAD,∴AB![]() PD,
PD,
在ΔPCD内,E、F分别是PC、CD的中点,EF//PD, ∴ AB![]() EF.
EF.
由此得![]() 平面
平面![]() .
.
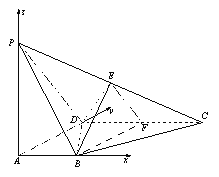
(Ⅱ)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,
则![]()
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
则 
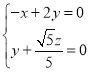 可取
可取![]()
设二面角EBDC的大小为![]() ,则
,则
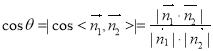 =
=![]() ,
,
所以,![]()


科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条。假定这种围巾的销售量t(条)是售价x(元)(![]() )的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(![]() )的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采用招考方式引进人才,规定必须在![]() ,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 测试合格的概率分别为
测试合格的概率分别为![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学在高考前各做了5次立定跳远测试,测得甲的成绩如下(单位:米):2.20,2.30,2.30,2.40,2.30,若甲、乙两人的平均成绩相同,乙的成绩的方差是0.005,那么甲、乙两人成绩较稳定的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
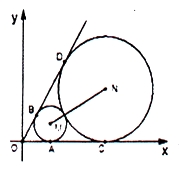
【题目】如图,已知圆心坐标为![]() 的圆
的圆![]() 与
与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点,另一圆
两点,另一圆![]() 与圆
与圆![]() 外切,且与
外切,且与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点.
两点.
(1)求圆![]() 和圆
和圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 的平行线
的平行线![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得的弦的长度.
截得的弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)试证明函数![]() 是偶函数;
是偶函数;
(2)画出![]() 的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
(3)请根据图象指出函数![]() 的单调递增区间与单调递减区间;(不必证明)
的单调递增区间与单调递减区间;(不必证明)
(4)当实数![]() 取不同的值时,讨论关于
取不同的值时,讨论关于![]() 的方程
的方程![]() 的实根的个数;(不必求出方程的解)
的实根的个数;(不必求出方程的解)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com