Question

10．如图：平面直角坐标系中p（x，y）（y≠0）为一动点，A（-1，0），B（2，0）∠PBA=2∠PAB．
（1）求动点P轨迹E的方程；
（2）过E上任意一P（x₀，y₀）向（x+1）²+y²=1作两条切线PF、PR，且PF、PR交y轴于M、N，求MN长度的取值范围．

Answer 1

分析 （1）由题意可得tan∠PBA=$\frac{-y}{x-2}$，tan∠PAB=$\frac{y}{x+1}$，再根据tan∠PBA=tan2∠PAB=$\frac{2tan∠PAB}{1{-tan}^{2}∠PAB}$，化简可得点P的轨迹方程．
（2）设PF斜率为k₁，PR斜率为k₂，求得PF和PR的方程，可得|MN|=（k₁-k₂）x₀|，再根据直线和圆相切的性质，k₁、k₂为 $\frac{{|y}_{0}-k{（x}_{0}+1）|}{\sqrt{{k}^{2}+1}}$=1的两个实数解，即（${{x}_{0}}^{2}$+2x₀）k²-2y₀（x₀+1）k+${{y}_{0}}^{2}$-1=0，利用韦达定理可得k₁+k₂ 和k₁•k₂，可得|MN|²=$\frac{4{{[y}_{0}}^{2}{{+x}_{0}}^{2}+{2x}_{0}]}{{{（x}_{0}+2）}^{2}}$=$\frac{4[{{4x}_{0}}^{2}+{2x}_{0}-3]}{{{（x}_{0}+2）}^{2}}$，再利用导数判断它的单调性，由单调性求出|MN|的范围．

解答 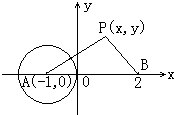解：（1）由题意可得tan∠PBA=-K_PB=$\frac{-y}{x-2}$，tan∠PAB=K_PA=$\frac{y}{x+1}$，
再根据∠PBA=2∠PAB，可得tan∠PBA=tan2∠PAB=$\frac{2tan∠PAB}{1{-tan}^{2}∠PAB}$，
即 $\frac{-y}{x-2}$=$\frac{\frac{2y}{x+1}}{1{-（\frac{y}{x+1}）}^{2}}$，化简可得 3x²-y²=3，即 x²-$\frac{{y}^{2}}{3}$=1 （x＞1）．
（2）设PF斜率为k₁，PR斜率为k₂，
则PF：y-y₀=k₁（x-x₀），PR：y-y₀=k₂（x-x₀），
令x=0，可得y_M=y₀-k₁x₀，y_N=y₀-k₂x₀，∴|MN|=（k₁-k₂）x₀|，
由PF和圆相切得：$\frac{|{-k}_{1}{+y}_{0}{{-k}_{1}x}_{0}|}{\sqrt{{{k}_{1}}^{2}+1}}$=1，PR和圆相切得：$\frac{|{-k}_{2}{+y}_{0}{{-k}_{2}x}_{0}|}{\sqrt{{{k}_{2}}^{2}+1}}$=1，
故：k₁、k₂为 $\frac{{|y}_{0}-k{（x}_{0}+1）|}{\sqrt{{k}^{2}+1}}$=1的两个实数解，
故有：（${{x}_{0}}^{2}$+2x₀）k²-2y₀（x₀+1）k+${{y}_{0}}^{2}$-1=0，利用韦达定理可得k₁+k₂=$\frac{{2y}_{0}{（x}_{0}+1）}{{{x}_{0}}^{2}+{2x}_{0}}$，k₁•k₂=$\frac{{{y}_{0}}^{2}-1}{{{x}_{0}}^{2}+{2x}_{0}}$．                             
|MN|²=${{x}_{0}}^{2}$[${{（k}_{1}{+k}_{2}）}^{2}$-4k₁•k₂]=${{x}_{0}}^{2}$[${{（k}_{1}{+k}_{2}）}^{2}$-4k₁•k₂]=$\frac{4{{[y}_{0}}^{2}{{+x}_{0}}^{2}+{2x}_{0}]}{{{（x}_{0}+2）}^{2}}$，
又∵${{x}_{0}}^{2}$-$\frac{{{y}_{0}}^{2}}{3}$=1，∴|MN|²=$\frac{4[{{4x}_{0}}^{2}+{2x}_{0}-3]}{{{（x}_{0}+2）}^{2}}$，
设g（x₀）=$\frac{4[{{4x}_{0}}^{2}+{2x}_{0}-3]}{{{（x}_{0}+2）}^{2}}$，则g′（x₀）=$\frac{8（{7x}_{0}+5）}{{{（x}_{0}+2）}^{3}}$ （x₀＞1），故g（x）在（1，+∞）上是增函数．
当x₀趋于1时，g（x₀）趋于$\frac{4}{3}$；当x₀趋于+∞时，g（x₀）趋于16，故|MN|²∈（$\frac{4}{3}$，16），
故|MN|的范围为（$\frac{2\sqrt{3}}{3}$，4）．

点评 本题主要考查直线的斜率公式，求动点的轨迹方程，直线和圆锥曲线的位置关系，利用导数研究函数的单调性，属于难题．