
| A. | 183 | B. | 132 | C. | 528 | D. | 732 |
分析 通过韦达定理可知an+an+1=-3n、an•an+1=bn,进而可知an+2-an=-3,通过n=1可知a2=-4,进而计算可得结论.
解答 解:∵an、an+1是方程x2+3nx+bn=0的两根,
∴an+an+1=-3n、an•an+1=bn,
∴an+2-an=-3,
∴a1,a3,a5,…和 a2,a4,a6…都是公差为-3的等差数列,
∴奇数项构成的数列为:{1,-2,-5,…},
偶数项构成的数列为:{-4,-7,-10,…},
∴b1+b2+b3+b4+b5+b6
=1×(-4)+(-4)×(-2)+(-2)×(-7)+(-7)×(-5)+(-5)×(-10)+(-10)×(-8)
=-4+8+14+35+50+80
=183,
∴4(b1+b2+b3+b4+b5+b6)=4×183=732,
故选:D.
点评 本题考查数列的通项,考查运算求解能力,分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0.
在矩形中ABCD中,AB=4,BC=2$\sqrt{3}$,M为动点,DM、CM的延长线与AB(或其延长线)分别交于点E、F,若$\overrightarrow{AE}$•$\overrightarrow{BF}$+$\overrightarrow{EF}$2=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
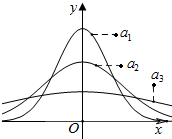 如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.
如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | ( 2,4 ) | C. | [-2,-1 ) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.
如图:平面直角坐标系中p(x,y)(y≠0)为一动点,A(-1,0),B(2,0)∠PBA=2∠PAB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ | B. | [kπ-$\frac{π}{3}$,kπ](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{2π}{3}$](k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com