
分析 先求出函数的导数(1)将a=1代入,求出f′(1)的值,从而求出切线方程;
(2)通过讨论a的范围,求出f′(x)的符号,从而得到函数的单调性.
解答 解 f′(x)=x-$\frac{2a}{x}$+a-2=$\frac{(x-2)(x+a)}{x}$,(x>0),
(1)当a=1时,f′(x)=$\frac{(x-2)(x+1)}{x}$,f′(1)=-2,
∴所求的切线方程为y-f(1)=-2(x-1),即4x+2y-3=0.
(2)①当-a=2,即a=-2时,f′(x)=$\frac{{(x-2)}^{2}}{x}$≥0,f(x)在(0,+∞)上单调递增;
②当-a<2,即-2<a<0时,∵0<x<-a或x>2时,f′(x)>0;-a<x<2时,f′(x)<0,
f(x)在(0,-a),(2,+∞)上单调递增,在(-a,2)上单调递减;
③当-a>2,即a<-2时,∵0<x<2或x>-a时,f′(x)>0;
2<x<-a时,f′(x)<0,f(x)在(0,2),(-a,+∞)上单调递增,在(2,-a)上单调递减,
综上a=-2时,f(x)在(0,+∞)上单调递增.
-2<a<0时,f(x)在(0,-a),(2,+∞)上单调递增,在(-a,2)上单调递减,
a<-2时,f(x)在(0,2),(-a,+∞)上单调递增,在(2,-a)上单调递减.
点评 本题考查了曲线的切线方程问题,考查函数的单调性问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-3,3) | C. | (-2,2) | D. | (-4,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 183 | B. | 132 | C. | 528 | D. | 732 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(cos2)>f(sin1)>f(sin$\frac{1}{2}$) | B. | f(cos2)>f(sin$\frac{1}{2}$)>f(sin1) | ||
| C. | f(sin$\frac{1}{2}$)>f(cos2)>f(sin1) | D. | f(sin1)>f(sin$\frac{1}{2}$)>f(cos2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
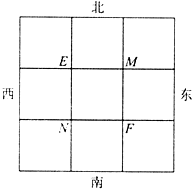 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com