
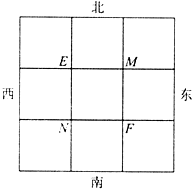
 ��֪�ס������˷ֱ�λ��ͼ�е�M��N���㣬ÿ��1���ӣ��ס������˷ֱ����������ĸ����������һ����������1���Ҽ����ĸ��������ߵĸ�������ȵģ������������ߵĸ��ʶ���$\frac{1}{3}$�������ߵĸ�����$\frac{1}{4}$���ס��ҷֱ���ij���������ߵ��¼���ΪA��B��
��֪�ס������˷ֱ�λ��ͼ�е�M��N���㣬ÿ��1���ӣ��ס������˷ֱ����������ĸ����������һ����������1���Ҽ����ĸ��������ߵĸ�������ȵģ������������ߵĸ��ʶ���$\frac{1}{3}$�������ߵĸ�����$\frac{1}{4}$���ס��ҷֱ���ij���������ߵ��¼���ΪA��B������ ��1�����ݼ����ĸ��������ߵĸ�������ȵģ��ʼ��������ߵĸ��ʣ���1��ȥ�������ϡ������ߵĸ��ʣ��������������ߵĸ��ʣ�
��2������������¼��ĸ��ʳ˷���ʽ����ڵ�E�����ĸ��ʺ��ڵ�F�����ĸ��ʣ���Ӽ�������
��� �⣺��1�����ڼ����ĸ��������ߵĸ�������ȵģ��ʼ��������ߵĸ���Ϊ$\frac{1}{4}$��
���������ߵĸ���Ϊ1-$\frac{1}{3}$-$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{12}$��
��2�������˾���1���������ĵص���ͼ�е�E��� F���ڵ�E�����ĸ���Ϊ $\frac{1}{4}��\frac{1}{4}$=$\frac{1}{16}$���ڵ�F�����ĸ���Ϊ$\frac{1}{4}��\frac{1}{3}$=$\frac{1}{12}$��
�����˾���1���������ĸ���Ϊ $\frac{1}{16}$+$\frac{1}{12}$=$\frac{7}{48}$��
���� ������Ҫ����������¼��ĸ��ʳ˷���ʽ��Ӧ�ã������˷������۵���ѧ˼�룬���ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 3 | C�� | $\frac{25}{9}$ | D�� | $\frac{17}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[{k��+\frac{��}{6}��k��+\frac{2��}{3}}]��k��Z��$ | B�� | [k��-$\frac{��}{3}$��k��]��k��Z�� | C�� | [k��+$\frac{��}{6}$��k��+$\frac{��}{3}$]��k��Z�� | D�� | [k��+$\frac{��}{3}$��k��+$\frac{2��}{3}$]��k��Z�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|0��x��2} | B�� | {x|-2��x��0} | C�� | {1��2} | D�� | {-2��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$��
��֪����f��x��=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com