
| A. | 1 | B. | 3 | C. | $\frac{25}{9}$ | D. | $\frac{17}{9}$ |
分析 先根据对称性得到a,b的关系,代入$\frac{1}{a}$+$\frac{8}{b}$利用基本不等式求出最小值即可.
解答 解:设A(a,b)关于直线x+y-2=0的对称点B(x0,y0)在直线2x+y+3=0上,
∴线段AB的中点($\frac{a{+x}_{0}}{2}$,$\frac{b{+y}_{0}}{2}$)在直线x+y-2=0上,
由题意得:$\left\{\begin{array}{l}{{2x}_{0}{+y}_{0}+3=0}\\{{K}_{AB}=\frac{{y}_{0}-b}{{x}_{0}-a}}\\{\frac{a{+x}_{0}}{2}+\frac{b{+y}_{0}}{2}-2=0}\end{array}\right.$,∴a+2b=9,
∴$\frac{1}{a}$+$\frac{8}{b}$=$\frac{a+2b}{9a}$+$\frac{8a+16b}{9b}$=$\frac{17}{9}$+$\frac{2b}{9a}$+$\frac{8a}{9b}$≥$\frac{17}{9}$+2$\sqrt{\frac{2b}{9a}•\frac{8a}{9b}}$=$\frac{25}{9}$,
当且仅当:$\frac{2b}{9a}$=$\frac{8a}{9b}$即b=2a时“=”成立,
故选:C.
点评 本题考查了基本不等式的性质,考查图象的对称性,是一道中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-3,3) | C. | (-2,2) | D. | (-4,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(cos2)>f(sin1)>f(sin$\frac{1}{2}$) | B. | f(cos2)>f(sin$\frac{1}{2}$)>f(sin1) | ||
| C. | f(sin$\frac{1}{2}$)>f(cos2)>f(sin1) | D. | f(sin1)>f(sin$\frac{1}{2}$)>f(cos2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
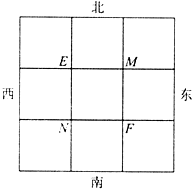 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com