
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,连接BH,则∠ABH=α,就是AB在平面BCD所成角,解直角三角形ABH即可.
解答  解:如图:在等边三角形BCD中,BM为CD边上的高,再在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,则∠ABH=α,就是AB在平面BCD所成角,
解:如图:在等边三角形BCD中,BM为CD边上的高,再在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,则∠ABH=α,就是AB在平面BCD所成角,
设棱长为a,由BM为CD边上的高,
则BM=$\frac{\sqrt{3}}{2}a$,在Rt△ABH中,则BH=$\frac{2}{3}$BM
=a$•\frac{\sqrt{3}}{2}×\frac{2}{3}=\frac{\sqrt{3}}{3}a$,
∴cosα=$\frac{BH}{AB}=\frac{\frac{\sqrt{3}}{3}a}{a}=\frac{\sqrt{3}}{3}$.
故选:D.
点评 本题考查了直线与平面所成的角,关键是找到斜线在平面内的射影,把空间角转化为平面角求解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
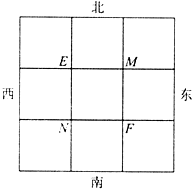 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com