
分析 (1)根据题意,分2步进行分析:①、先将甲、乙两人安排在两头,②将其余5人全排列,安排在中间5个位置,由分步计数原理计算可得答案;
(2)根据题意,分2步进行分析,①、将男生看成一个元素,考虑3人之间的顺序,②、将3名男生的整体与4名女生进行全排列,由分步计数原理计算可得答案;
(3)根据题意,分2步进行分析,①、将4名女生进行全排列,②、排好后有5个空位,在5个空位中任选3个,安排3名男生,由分步计数原理计算可得答案;
(4)根据题意,分3步进行分析,①、先安排甲乙2人,考虑其顺序,②、在剩余的5人中任选1人,排在甲乙2人之间,③、将3人看成一个元素,与剩余的4人进行全排列,由分步计数原理计算可得答案.
解答 解:(1)甲、乙两人必须站在两头,则先将甲乙2人安排在两端,有A22=2种方法,
其余5人站在中间5个位置,有A55=120种方法,
根据乘法原理可得,不同的排列方法共有2×120=240种;
(2)将男生看成一个元素,考虑3人之间的顺序,有A33=6种顺序,
将3名男生的整体与4名女生进行全排列,有A55=120种方法,
则男生必须排在一起的排法有6×120=720种;
(3)将4名女生进行全排列,有A44=24种顺序,
排好后有5个空位,在5个空位中任选3个,安排3名男生,有A53=60种情况,
则男生互不相邻的排法有24×60=1440种;
(4)先安排甲乙2人,有A22=2种方法,
在剩余的5人中任选1人,排在甲乙2人之间,有5种情况,
将3人看成一个元素,与剩余的4人进行全排列,有A55=120种排法;
则甲、乙两人之间恰好间隔1人有2×5×120=1200种排法.
点评 本题主要考查了排列组合的运用,需要注意常见问题中的处理方法,特殊元素优先安排,相邻问题用捆绑法,不相邻问题用插空法,正难则反,运用排除法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
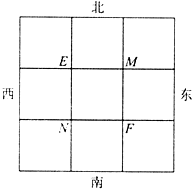 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com