
【题目】设集合![]() 由满足下列两个条件的数列
由满足下列两个条件的数列![]() 构成:①
构成:①![]() ②存在实数
②存在实数![]() 使得
使得![]() 对任意正整数
对任意正整数![]() 都成立.
都成立.
(1)现在给出只有5项的有限数列![]() 试判断数列
试判断数列![]() 是否为集合
是否为集合![]() 的元素;
的元素;
(2)设数列![]() 的前项和为
的前项和为![]() 且
且![]() 若对任意正整数
若对任意正整数![]() 点
点![]() 均在直线
均在直线![]() 上,证明:数列
上,证明:数列![]() 并写出实数
并写出实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 若数列
若数列![]() 没有最大值,求证:数列
没有最大值,求证:数列![]() 一定是单调递增数列。
一定是单调递增数列。
【答案】(1)不是;(2)![]() ,
,![]() ;(3)证明略
;(3)证明略
【解析】
(1)由于![]() ,可知数列
,可知数列![]() 不满足条件①.(2)由于点
不满足条件①.(2)由于点![]() ,
,![]() 在直线
在直线
![]() 上,可得
上,可得![]() ,利用递推关系可得:
,利用递推关系可得:![]() ,利用等比数列的前
,利用等比数列的前![]() 项和公式可得:
项和公式可得:![]() ,验证
,验证![]() ,可知:条件①成立.由于
,可知:条件①成立.由于![]() ,即可得出条件②及其
,即可得出条件②及其![]() ,
,![]() 的范围.(3)利用反证法证明.
的范围.(3)利用反证法证明.
(1)解:![]()
![]() ,因此数列
,因此数列![]() 不满足条件①,
不满足条件①,![]() 数列
数列![]() .
.
(2)证明:![]() 点
点![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,
,
当![]() 时,
时,![]() ,可得:
,可得:![]() ,化为
,化为![]() ,
,
n=1时,易知![]() ,显然
,显然![]()
![]() 数列
数列![]() 是等比数列,首项为1,公比为
是等比数列,首项为1,公比为![]() .
.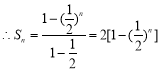 ,
,
则![]() ,
,
![]()
![]() .
.![]() 条件①成立.
条件①成立.
由于![]() ,
,![]() ,
,![]() .
.
(3)证明:(反证法)若数列![]() 非单调递增,则一定存在正整数
非单调递增,则一定存在正整数![]() ,使
,使![]() 成立,
成立,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
而![]() ,所以
,所以![]() .
.
显然在![]() ,
, ![]() ,
,![]() ,
,![]() 这
这![]() 项中一定存在一个最大值,不妨记为
项中一定存在一个最大值,不妨记为![]() ,
,
所以为![]() ,这与数列
,这与数列![]() 没有最大值相矛盾.
没有最大值相矛盾.
所以假设不成立,故命题得证.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了应对金融危机,决定适当进行裁员,已知这家公司现有职工![]() 人(
人(![]() ,且
,且![]() 为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员
为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员
千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
(1)设公司裁员人数为![]() ,写出公司获得的经济效益
,写出公司获得的经济效益![]() (千元)关于
(千元)关于![]() 的函数(经济效益=在职人员创利总额—被裁员工生活费);
的函数(经济效益=在职人员创利总额—被裁员工生活费);
(2)为了获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
科目:高中数学 来源: 题型:
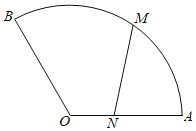
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com