
【题目】已知函数f(x)=|x﹣a|,g(x)= ![]() ,若方程f(x)=g(x)﹣a有且只有一个实数根,则实数a的取值集合为 .
,若方程f(x)=g(x)﹣a有且只有一个实数根,则实数a的取值集合为 .
【答案】(﹣1,+∞)
【解析】解:方程f(x)=g(x)﹣a有且只有一个实数根, 即|x﹣a|= ![]() ﹣a有且只有一个实数根,
﹣a有且只有一个实数根,
也就是|x﹣a|+a= ![]() 有且只有一个实数根,
有且只有一个实数根,
令h(x)=|x﹣a|+a,t(x)= ![]() .
.
若a=0,则h(x)=|x|,作出函数图象如图1:
方程f(x)=g(x)﹣a有且只有一个实数根;
若a>0,函数h(x)是把函数y=|x|的图象向右向上平移a个单位得到,
作出函数h(x)与t(x)的图象如图2:
对于任意a>0,方程f(x)=g(x)﹣a有且只有一个实数根;
若a<0,函数h(x)是把函数y=|x|的图象向左向下平移|a|个单位得到,
作出函数h(x)与t(x)的图象如图3:
要使方程f(x)=g(x)﹣a有且只有一个实数根,则﹣1<a<0.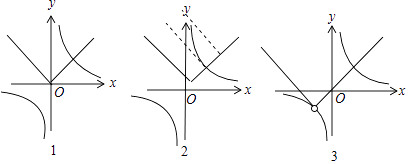
综上,实数a的取值集合为(﹣1,+∞).
所以答案是:(﹣1,+∞).


科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表数据:
单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为 ![]() =﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
=﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
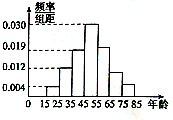
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax4lnx+bx4﹣c在x=1处取得极值﹣3﹣c.
(1)试求实数a,b的值;
(2)试求函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中S的值不可以用算法求解的是( )
A.S=1+2+3+4
B.S=1+2+3+4+…
C.S=1+ ![]() +
+ ![]() +…+
+…+ ![]()
D.S=12+22+32+…+1002
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=x0与g(x)=1
B.f(x)=x与g(x)= ![]()
C.f(x)=x2﹣1与g(x)=x2+1
D.f(x)=|x|与g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x+y)=f(x)+f(y)且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
A.f(1)+2f(1)+…+nf(1)
B.f( ![]() )
)
C.n(n+1)
D.n(n+1)f(1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com