
【题目】已知函数f(x)=ax4lnx+bx4﹣c在x=1处取得极值﹣3﹣c.
(1)试求实数a,b的值;
(2)试求函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求实数c的取值范围.
【答案】
(1)解:由题意知f(1)=﹣3﹣c,因此b﹣c=﹣3﹣c,从而b=﹣3
又对f(x)求导得f′(x)=x3(4alnx+a+4b)
由题意f'(1)=0,因此a+4b=0,解得a=12
(2)解:由(1)知f'(x)=48x3lnx(x>0),令f'(x)=0,解得x=1
当0<x<1时,f'(x)<0,此时f(x)为减函数;
当x>1时,f'(x)>0,此时f(x)为增函数
因此f(x)的单调递减区间为(0,1),而f(x)的单调递增区间为(1,+∞)
(3)解:由(II)知,f(x)在x=1处取得极小值f(1)=﹣3﹣c,此极小值也是最小值,
要使f(x)≥﹣2c2(x>0)恒成立,只需﹣3﹣c≥﹣2c2
即2c2﹣c﹣3≥0,从而(2c﹣3)(c+1)≥0,解得c≥ ![]() 或c≤﹣1
或c≤﹣1
所以c的取值范围为(﹣∞,﹣1]∪[ ![]() ,+∞)
,+∞)
【解析】(1)因为x=1时函数取得极值得f(x)=﹣3﹣c求出b,然后令导函数=0求出a即可;(2)解出导函数为0时x的值讨论x的取值范围时导函数的正负决定f(x)的单调区间;(3)不等式f(x)≥﹣2c2恒成立即f(x)的极小值≥﹣2c2 , 求出c的解集即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c.
(1)若a=2 ![]() ,A=
,A= ![]() ,且△ABC的面积S=2
,且△ABC的面积S=2 ![]() ,求b,c的值;
,求b,c的值;
(2)若sin(C﹣B)=sin2B﹣sinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x﹣1)=﹣f(﹣x+1),且当x≤0时,f(x)=x3 , 若对任意的x∈[t,t+2],不等式f(x+t)≥2 ![]() f(x)恒成立,则实数t的取值范围是 .
f(x)恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b是实数,函数f(x)=x|x﹣a|+b.
(1)当a=2时,求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[1,2]上的最大值;
(3)若存在a∈[﹣3,0],使得函数f(x)在[﹣4,5]上恒有三个零点,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知复平面内平行四边形ABCD中,点A对应的复数为﹣1, ![]() 对应的复数为2+2i,
对应的复数为2+2i, ![]() 对应的复数为4﹣4i.
对应的复数为4﹣4i.
(Ⅰ)求D点对应的复数;
(Ⅱ)求平行四边形ABCD的面积.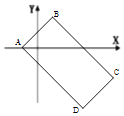
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示. (Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?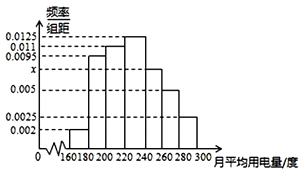
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com