
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.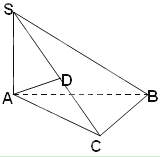
(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.
见解析。
解析试题分析:(I)通过证明BC⊥AD,通过AD⊥SC,BC∩SC=C,证明AD⊥平面SBC;
(II)过D作DE∥BC,交SB于E,E点即为所求.直接利用直线与平面平行的判定定理即可证明BC∥平面ADE.
(Ⅰ)证明: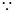 BC⊥平面SAC,AD
BC⊥平面SAC,AD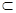 平面SAC,∴BC⊥AD,
平面SAC,∴BC⊥AD,
又∵AD⊥SC,
BC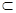 平面SBC, SC
平面SBC, SC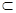 平面SBC,
平面SBC,
BC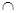 SC=C,
SC=C,
∴AD⊥平面SBC. …………(6分)
(Ⅱ)过A作AE⊥SB,交SB于E,E点即为所求.
∵AD⊥平面SBC,SB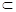 平面SBC,
平面SBC,
∴AD⊥SB.
又AE⊥SB,AE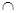 AD=A
AD=A
∴SB⊥平面ADE,又SB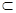 平面ABS,由两个平面垂直的判定定理知:
平面ABS,由两个平面垂直的判定定理知:
平面ABS⊥平面ADE…………(13分)考点:本题主要考查了直线与平面垂直,直线与平面平行的判定定理的应用,考查空间想象能力,逻辑推理能力.
点评:解决该试题的关键是熟练的运用线面垂直的判定定理和面面垂直的判定定理来证明命题的成立。


科目:高中数学 来源: 题型:解答题
(本题满分12分)
如图所示的几何体是由以正三角形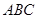 为底面的直棱柱被平面
为底面的直棱柱被平面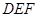 所截而得.
所截而得. 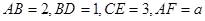 ,
, 为
为 的中点.
的中点.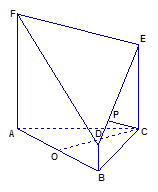
(1)当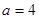 时,求平面
时,求平面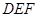 与平面
与平面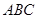 的夹角的余弦值;
的夹角的余弦值;
(2)当 为何值时,在棱
为何值时,在棱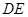 上存在点
上存在点 ,使
,使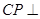 平面
平面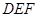 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.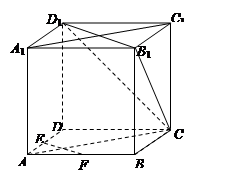
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)在四棱锥 中,底面ABCD是边长为1的正方形,
中,底面ABCD是边长为1的正方形, 平面ABCD,PA=AB,M,N分别为PB,AC的中点,
平面ABCD,PA=AB,M,N分别为PB,AC的中点,
(1)求证:MN //平面PAD (2)求点B到平面AMN的距离
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
(本题满分12分)
如图,已知三棱锥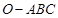 的侧棱
的侧棱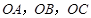 两两垂直,
两两垂直,
且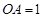 ,
, ,
,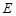 是
是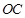 的中点。
的中点。
(1)求异面直线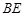 与
与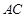 所成角的余弦值;
所成角的余弦值;
(2)求直线BE和平面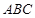 的所成角的正弦值。
的所成角的正弦值。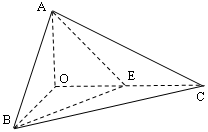
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图, 、
、 分别是正三棱柱
分别是正三棱柱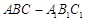 的棱
的棱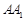 、
、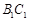 的中点,且棱
的中点,且棱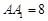 ,
, .
.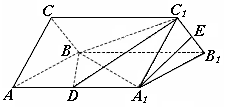
(Ⅰ)求证: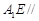 平面
平面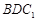 ;
;
(Ⅱ)在棱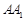 上是否存在一点
上是否存在一点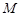 ,使二面角
,使二面角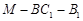 的大小为
的大小为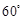 ,若存在,求
,若存在,求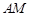 的长;若不存在,说明理由。
的长;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com