设数列{an}满足:an(n∈N*)是整数,且an+1-an是关于x的方程x2+(an+1-2)x-2an+1=0的根.
(1)若a1=4且n≥2时,4≤an≤8求数列{an}的前100项和S100;
(2)若a1=-8,a6=1且an<an+1(n∈N*)求数列{an}的通项公式.
解:(1)∵a
n+1-a
n是关于x的方程x
2+(a
n+1-2)x-2a
n+1=0的根
∴(a
n+1-a
n)
2+(a
n+1-2)(a
n+1-a
n)-2a
n+1=0
∴(a
n+1-a
n-2)(2a
n+1-a
n)=0
∴a
n+1=a
n+2,或a
n+1=

a
n,
∵a
1=4且n≥2时,4≤a
n≤8,
∴数列{a
n}为:4,6,8,4,6,8,…,
∴数列{a
n}的前100项和S
100=33(4+6+8)+8=598;
(2)若a
1=-8且a
n<a
n+1(n∈N
*)
∵a
n+1=a
n+2,或a
n+1=

a
n,
∴数列{a
n}的前6项是:-8,-6,-4,-2,0,2或-8,-6,-4,-2,-1,1或:-8,-6,-3,-1,1,3或-8,-6,-2,0,2,4或-8,-6,-2,-1,1,3
∵a
6=1,∴数列{a
n}的前6项是-8,-6,-4,-2,-1,1,且n>4时,a
n+1=a
n+2,
∴数列{a
n}的通项公式是
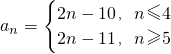
;
分析:(1)利用a
n+1-a
n是关于x的方程x
2+(a
n+1-2)x-2a
n+1=0的根,可得a
n+1=a
n+2,或a
n+1=

a
n,结合a
1=4且n≥2时,4≤a
n≤8,即可得到结论;
(2)根据条件,确定数列{a
n}的前6项是-8,-6,-4,-2,-1,1,且n>4时,a
n+1=a
n+2,从而可得数列{a
n}的通项公式.
点评:本题考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

 an,
an, an,
an,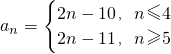 ;
; an,结合a1=4且n≥2时,4≤an≤8,即可得到结论;
an,结合a1=4且n≥2时,4≤an≤8,即可得到结论;

 名校课堂系列答案
名校课堂系列答案