
����Ŀ���жϾ����Ƿ�С����һ����Ҫָ���Ǿ��������룬ij�д�Ͻ���������ȡ100��������ÿ��������������������������з��������i������������xi����Ԫ���������yi����Ԫ�����������ݴ����ģ� ![]() =400��
=400�� ![]() =100��
=100�� ![]() =900��
=900�� ![]() =2850��
=2850��
��1����֪��ͥ�������y��������x����������ع�ϵ�������Իع鷽�̣�
��2�������еľ�����������5���Ƹþ����Ѵ�С�������Ԥ����ﵽС����������������ӦΪ������Ԫ�� ������y=bx+a�У�b= 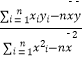 ��a=
��a= ![]() ������
������ ![]() ��
�� ![]() Ϊ����ƽ��ֵ��
Ϊ����ƽ��ֵ��
 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ�����{an}�ǵ������������У�a2+a3+a4=28����a3+2��a2 �� a4�ĵȲ����
��1��������{an}��ͨ�ʽ��
��2����bn=anlog2an �� ����{bn}��ǰn���ΪSn �� ��Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3��3x��
��1��������y=f��x���ڵ�x=2�������߷��̣�
��2��������A��1��m����m�٩�2����������y=f��x�����������ߣ���ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ���ֱ�����Բ
���ֱ�����Բ![]() �����ҽ���.
�����ҽ���.
��1������![]() �ǵ�һ��������Բ�ϵ�һ�㣬
�ǵ�һ��������Բ�ϵ�һ�㣬 ![]() ,���
,���![]() �����ꣻ
�����ꣻ
��2���������![]() ��ֱ��
��ֱ��![]() ����Բ���ڲ�ͬ������
����Բ���ڲ�ͬ������![]() ����
����![]() Ϊ��ǣ�����
Ϊ��ǣ�����![]() Ϊ����ԭ�㣩����ֱ��
Ϊ����ԭ�㣩����ֱ��![]() ��б��
��б��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֳ���������![]() ��
��![]() �����ͺŵĻ�Ƥ����900�ֲָģ�
�����ͺŵĻ�Ƥ����900�ֲָģ�![]() ��
��![]() ���ֳ�Ƥ���ػ����ֱ�Ϊ36�ֺ�60�֣����ֱ�Ϊ1.6��Ԫ/����2.4��Ԫ/�����ֳ�Ҫ���Ƥ����������21������
���ֳ�Ƥ���ػ����ֱ�Ϊ36�ֺ�60�֣����ֱ�Ϊ1.6��Ԫ/����2.4��Ԫ/�����ֳ�Ҫ���Ƥ����������21������![]() �ͳ�Ƥ������
�ͳ�Ƥ������![]() �ͳ�Ƥ7�����ֱ���
�ͳ�Ƥ7�����ֱ���![]() ��
��![]() ��ʾ����
��ʾ����![]() ��
��![]() ���ֳ�Ƥ�ĸ���.
���ֳ�Ƥ�ĸ���.
��1����![]() ��
��![]() �г�������������ѧ��ϵʽ����������Ӧ��ƽ������
�г�������������ѧ��ϵʽ����������Ӧ��ƽ������
��2���ֱ�����![]() ��
��![]() ���ֳ�Ƥ�ĸ����Ƕ���ʱ������ʹ��������٣����������С���.
���ֳ�Ƥ�ĸ����Ƕ���ʱ������ʹ��������٣����������С���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ,
,![]() ��֪����y=f(x)
��֪����y=f(x)
��![]() ����������ֱ��
����������ֱ��![]() ��ֱ��
��ֱ��
(1) ��![]() ��ֵ��
��ֵ��
(2) ��������x��1������![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧͬʱ���������ӣ��õ������ֱ�Ϊa��b������Բ ![]() =1��a��b��0����������e��
=1��a��b��0����������e�� ![]() �ĸ����ǣ� ��
�ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=log2��ax2+4x+5����
��1����f��1����3����a��ȡֵ��Χ��
��2����a=1������f��x����ֵ��
��3����f��x����ֵ��ΪR����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3+ax2+bx+c��x=�� ![]() ��x=1ʱ��ȡ�ü�ֵ��
��x=1ʱ��ȡ�ü�ֵ��
��1����a��b��ֵ�뺯��f��x���ĵ������䣻
��2������x��[��1��2]������ʽf��x����c2���������c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com