
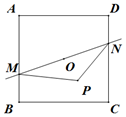
 正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )| A. | $-\frac{3}{4}$ | B. | -1 | C. | $-\frac{7}{4}$ | D. | -2 |
分析 根据$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$得出2$\overrightarrow{OP}$的终点在线段BC上,即|2$\overrightarrow{OP}$|≥1,求出${\overrightarrow{OP}}^{2}$≥$\frac{1}{4}$;又O是MN的中点,得出$\overrightarrow{OM}$+$\overrightarrow{ON}$=$\overrightarrow{0}$,$\overrightarrow{OM}$•$\overrightarrow{ON}$≥$\sqrt{2}$×$\sqrt{2}$×cosπ,求$\overrightarrow{PM}•\overrightarrow{PN}$=($\overrightarrow{OM}$-$\overrightarrow{OP}$)•($\overrightarrow{ON}$-$\overrightarrow{OP}$)的最小值即可.
解答 解:根据题意,$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,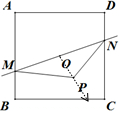
∴2$\overrightarrow{OP}$的终点在线段BC上,
∴|2$\overrightarrow{OP}$|≥1,
∴|$\overrightarrow{OP}$|≥$\frac{1}{2}$,
∴${\overrightarrow{OP}}^{2}$≥$\frac{1}{4}$;
又O是MN的中点,
∴$\overrightarrow{OM}$+$\overrightarrow{ON}$=$\overrightarrow{0}$,
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$≥$\sqrt{2}$×$\sqrt{2}$×cosπ=-2,
∴$\overrightarrow{PM}•\overrightarrow{PN}$=($\overrightarrow{OM}$-$\overrightarrow{OP}$)•($\overrightarrow{ON}$-$\overrightarrow{OP}$)
=$\overrightarrow{OM}$•$\overrightarrow{ON}$-$\overrightarrow{OP}$•($\overrightarrow{OM}$+$\overrightarrow{ON}$)+${\overrightarrow{OP}}^{2}$≥-2-0+$\frac{1}{4}$=-$\frac{7}{4}$,
∴$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值是-$\frac{7}{4}$.
故选:C.
点评 本题考查了平面向量的数量积运算性质、向量的三角形法则、向量共线定理应用问题,是中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$,M为AB中点,N为BD靠近B的三等分点.
已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$,M为AB中点,N为BD靠近B的三等分点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不使用手机 | 使用手机 | 合计 | |
| 学习成绩优秀人数 | 18 | 7 | 25 |
| 学习成绩不优秀人数 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com