
| 不使用手机 | 使用手机 | 合计 | |
| 学习成绩优秀人数 | 18 | 7 | 25 |
| 学习成绩不优秀人数 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)计算观测值K2,对照临界值即可得出结论;
(2)利用列举法求基本事件数,计算对应的概率值.
解答 解:(1)根据上方公式求得
K2=$\frac{50{×(18×19-6×7)}^{2}}{24×26×25×25}$=11.538>10.828,
所以该研究小组有99.9%的把握认为,
中学生使用手机对学习有影响;…(5分)
(2)记A组推选的两名同学分别为C、D,
B组推选的三名同学分别为a、b、c,
则从这5人中任取两人有
CD、Ca、Cb、Cc、Da、Db、Dc、ab、ac、bc,共10种取法,
其中一人来自A组、另一人来自B组有6种取法,
故挑选的两人中一人来自A组、另一人来自B组的概率为
P=$\frac{6}{10}$=$\frac{3}{5}$.…(12分)
点评 本题考查了独立性检验和列举法求古典概型的概率问题,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
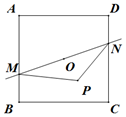 正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )| A. | $-\frac{3}{4}$ | B. | -1 | C. | $-\frac{7}{4}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2100 | B. | 24950 | C. | 25050 | D. | 25151 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
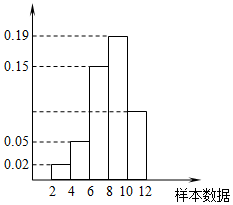 有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )| A. | 27 | B. | 81 | C. | 54 | D. | 108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com