
分析 (1)利用正弦函数的周期性求得ω的值,可得函数f(x)的解析式;
(2)利用正弦函数的定义域和值域,求得函数y=g(x+$\frac{π}{3}$)-m 的最小值,根据它的最小值为2,求得实数m的值.
解答 解:(1)根据函数f(x)=2sinωπx,且函数f(x)的图象与y=-2的图象的相邻两交点的横坐标之差为2,
可得T=$\frac{2π}{ωπ}$=2,∴ω=1,f(x)=2sinπx.
(2)将函数f(x)的图象的横坐标扩大π倍得到函数g(x)=2sinx的图象,
∵x∈[-$\frac{2π}{3}$,$\frac{5π}{6}$],∴x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{7π}{6}$],sin(x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],∴2sin(x+$\frac{π}{3}$)-m∈[-$\sqrt{3}$-m,2-m],
若函数y=g(x+$\frac{π}{3}$)-m=2sin(x+$\frac{π}{3}$)-m 在[-$\frac{2π}{3}$,$\frac{5π}{6}$]上的最小值为2,
则-$\sqrt{3}$-m=2,∴m=-$\sqrt{3}$-2.
点评 本题主要考查正弦函数的周期性,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 有一个解 | B. | 有两个解 | C. | 不能确定 | D. | 无解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f'(x)=\frac{sinx+cosx}{e^x}$ | B. | $f'(x)=-\frac{sinx+cosx}{e^x}$ | ||
| C. | $f'(x)=\frac{sinx-cosx}{e^x}$ | D. | $f'(x)=\frac{cosx-sinx}{e^x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
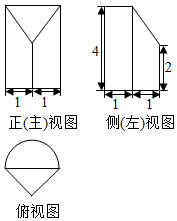 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3(π+1) | B. | 4π+1 | C. | π+$\frac{8}{3}$ | D. | 2π+$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
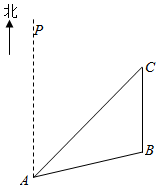 如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.
如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com