
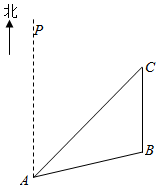
 如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.
如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.分析 (1)由诱导公式和正弦定理即可求出;
(2)先判断所在的位置,再根据余弦定理即可求出.
解答  (1)因为$cos∠PAB=\frac{7}{25}$,$cos∠PAC=\frac{3}{5}$,AB=2.5km,
(1)因为$cos∠PAB=\frac{7}{25}$,$cos∠PAC=\frac{3}{5}$,AB=2.5km,
所以在△ABC中,$cosB=-\frac{7}{25}$,$cosC=\frac{3}{5}$,
所以$sinB=\frac{24}{25}$,$sinC=\frac{4}{5}$,
$sinA=sin(B+C)=sinBcosC+cosBsinC=\frac{44}{125}$,
在△ABC中,由正弦定理$\frac{AB}{sinC}=\frac{BC}{sinA}=\frac{AC}{sinB}$
得:$BC=\frac{ABsinA}{sinC}=1.1(km)$,$AC=\frac{ABsinB}{sinC}=3(km)$
(2)半小时后,假设甲位于点D,则AB=2.5km,
假设乙位于点E,因为乙的路程为3km,大于2.5km,
故点应位于道路BC上,且CE=0.6km,
在△CDE中,由余弦定理得:DE2=DC2+CE2-2DC•CEcosC=0.52+0.62-2×0.5×0.6×0.6=0.52,
所以DE=0.5km.
点评 本题考查了正弦定理和余弦定理,培养了学生的运算能力和转化能力,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,2) | C. | (2,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-1<x≤1} | D. | {x|-2<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com