
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
分析 由向量共线的坐标表示列三角等式,求出tanα的值,再由α为锐角得到α的值.
解答 解:∵$\overrightarrow a$=(1-cosα,$\sqrt{3}}$),$\overrightarrow b$=(sinα,3)且$\overrightarrow a$∥$\overrightarrow b$,
∴3-3cosα=$\sqrt{3}$sinα,
即2sin($α+\frac{π}{6}$)=$\sqrt{3}$.
又α为锐角,
∴$α+\frac{π}{6}$=$\frac{π}{3}$.∴α=$\frac{π}{6}$
故选:A.
点评 共线问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若$\overrightarrow{a}$=(a1,a2),$\overrightarrow{b}$=(b1,b2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$?a1a2+b1b2=0,$\overrightarrow{a}$∥$\overrightarrow{b}$?a1b2-a2b1=0,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
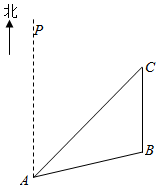 如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.
如图所示,某公园内从点A处出发有两条道路AB,AC连接到南北方向的道路BC.从点A处观察点B和点C的方位角分别是∠PAB和∠PAC,且cos∠PAB=$\frac{7}{25}$,cos∠PAC=$\frac{3}{5}$,AB=2.5km.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥1} | B. | {x|x>1} | C. | ∅ | D. | {x|x>1或x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S5•S6<0 | B. | H5•H6<0 | ||
| C. | 数列{an}、{Sn}都是单调递减数列 | D. | H6可能是数列{Hn}最大项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定是锐角三角形 | B. | 可能是直角三角形 | ||
| C. | 一定是钝角三角形 | D. | 可能是钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com