
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
分析 由题意,得到抽到的10人中,有男生4人,女生6人,再从这10位学生中随机抽取3人座谈,基本事件总数n=C${\;}_{10}^{3}$,3人中既有男生又有女生包含的基本事件个数m=${C}_{10}^{3}-{C}_{4}^{3}-{C}_{6}^{3}$,由此能求出3人中既有男生又有女生的概率.
解答 解:由题意,得到抽到的10人中,有男生4人,女生6人,
再从这10位学生中随机抽取3人座谈,
基本事件总数n=C${\;}_{10}^{3}$=120,
3人中既有男生又有女生包含的基本事件个数m=${C}_{10}^{3}-{C}_{4}^{3}-{C}_{6}^{3}$=120-4-20=96,
3人中既有男生又有女生的概率p=$\frac{m}{n}=\frac{96}{120}$=$\frac{4}{5}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题 | D. | ①是假命题,②是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
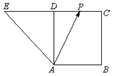 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )| A. | 3 | B. | $\frac{5}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com