
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,如图1,沿
的中点,如图1,沿![]() 将
将![]() 折起至
折起至![]() ,使
,使![]() ,如图2所示.
,如图2所示.
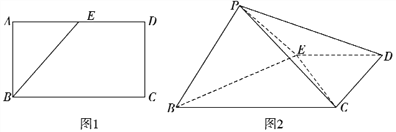
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由已知条件证明出![]() 平面
平面![]() ,根据面面垂直的判定定理证明出平面
,根据面面垂直的判定定理证明出平面![]() 平面
平面![]() ;(2)取BE的中点为
;(2)取BE的中点为![]() ,以
,以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,建立空间直角坐标系,写出各点坐标,设平面
轴,建立空间直角坐标系,写出各点坐标,设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,由线面垂直的性质定理,分别求出
,由线面垂直的性质定理,分别求出![]() 的坐标,求出二面角的余弦值。
的坐标,求出二面角的余弦值。
试题解析:
(1)证明:在图1中连接![]() ,则
,则![]()
![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]() .
.
(2)解:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,建立如图所示的直角坐标系,则
轴,建立如图所示的直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由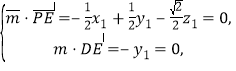 可得
可得![]() ;
;
由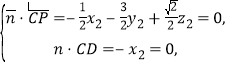 可得
可得![]() ;
;
则![]() ,由图形知二面角
,由图形知二面角![]() 的平面角为钝二面角,
的平面角为钝二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】某重点中学100位学生在市统考中的理科综合分数,以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在![]() 的学生中应抽取多少人?
的学生中应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点为坐标原点,焦点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是抛物线上的一点,以
是抛物线上的一点,以![]() 为圆心,2为半径的圆与
为圆心,2为半径的圆与![]() 轴相切,切点为
轴相切,切点为![]() .
.
(I)求抛物线的标准方程:
(Ⅱ)设直线![]() 在
在![]() 轴上的截距为6,且与抛物线交于
轴上的截距为6,且与抛物线交于![]() ,
,![]() 两点,连接
两点,连接![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数且
为常数且![]() ,令函数
,令函数![]() .
.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰为
的值域恰为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,点
中,点![]() 在
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,
上移动,![]() ,连接
,连接![]() .
.

(1)证明:对任意![]() ,总有
,总有![]() ∥平面
∥平面![]() ;
;
(2)当![]() 的长度最小时,求二面角
的长度最小时,求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体育公司对最近6个月内的市场占有率进行了统计,结果如表:

(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() ,
,![]() 两款车扩大市场,
两款车扩大市场,![]() ,
,![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:

平均每辆车每年可为公司带来收入500元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命都是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的期望值作为决策依据,应选择采购哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ;
;
回归直线方程![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com