
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析。
;(Ⅲ)见解析。
【解析】分析:(I)根据导数的几何意义求解即可.(II)分离参数,转化为![]() 恒成立求解.令
恒成立求解.令![]() ,可求得函数
,可求得函数![]() 的最大值为
的最大值为![]() ,进而可得结论.(III)由
,进而可得结论.(III)由![]() 分离参数可得
分离参数可得![]() ,借助(II)中的结论并结合函数
,借助(II)中的结论并结合函数![]() 的图象根据数形结合的方法可得函数零点的个数.
的图象根据数形结合的方法可得函数零点的个数.
详解:(I)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴所求切线方程为![]() ,
,
即![]() .
.
(II)由题意得![]() 恒成立等价于
恒成立等价于![]() 对
对![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减,
单调递减,
∴当![]() 时,
时,![]() 有最大值,且最大值为
有最大值,且最大值为![]() ,
,
∴![]() .
.
∴实数k的范围是![]() .
.
(III)由![]() ,即
,即![]() ,
,
得![]() ,
,
∴函数h(x)在区间![]() 上的零点个数即为函数
上的零点个数即为函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 上的公共点的个数.
上的公共点的个数.
由(II)得函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() 的最大值为
的最大值为![]() ,
,
又![]() ,
,![]() .
.
∴当![]() 或者
或者![]() 时,函数
时,函数![]() 有0个零点;
有0个零点;
当![]() 或者
或者![]() 时,函数
时,函数![]() 有1个零点;
有1个零点;
当![]() 时,函数
时,函数![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】给出以下结论,其中正确结论的个数为( )
①函数![]() 的零点为
的零点为![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() 时,函数值一定变号.
时,函数值一定变号.
②相邻两个零点之间的所有函数值保持同号.
③函数![]() 在区间
在区间![]() 上连续,若满足
上连续,若满足![]() ,则方程
,则方程![]() 在区间
在区间![]() 上一定有实根.
上一定有实根.
④“二分法”对连续不断的函数的所有零点都有效.
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中a∈R).
(其中a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由.
(2)若![]() ,试判断函数f(x)在区间[1,+∞)上的单调性,并用函数单调性定义给出证明.
,试判断函数f(x)在区间[1,+∞)上的单调性,并用函数单调性定义给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+![]() , g(x)=x+lnx,其中a>0,且x∈(0,+∞).
, g(x)=x+lnx,其中a>0,且x∈(0,+∞).
(1)若a=1,求f(x)的最小值;
(2)若对任意x≥1,不等式f(x)≤g(x)恒成立,求实数a的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,点
底面ABCD,点![]() 、F分别是线段
、F分别是线段![]() 、BC的中点.
、BC的中点.
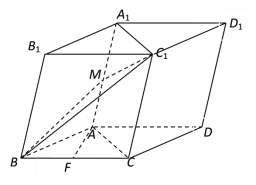
(1)求证:AF//平面![]() ;
;
(2)求证:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com