
分析 利用复数的运算法则、复数相等即可得出.
解答 解:a,b∈R,$\frac{a}{1-i}$+$\frac{b}{1-2i}$=$\frac{1+3i}{4}$,
∴$\frac{a(1+i)}{(1-i)(1+i)}$+$\frac{b(1+2i)}{(1-2i)(1+2i)}$=$\frac{a(1+i)}{2}$+$\frac{b(1+2i)}{5}$=$\frac{1+3i}{4}$,
化为:10a+10ai+4b+8bi=5+15i,
∴10a+4b=5,10a+8b=15,
解得a=-$\frac{1}{2}$,b=$\frac{5}{2}$.
则a+b=2.
故答案为:2.
点评 本题考查了复数的运算法则、复数相等,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{7}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
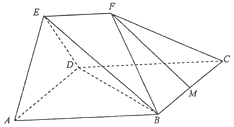 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西省高一上学期第一次月考数学试卷(解析版) 题型:解答题
已知函数f(x)在定义域R上满足 - f(x),当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4。
- f(x),当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4。
(1)求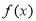 的解析式;
的解析式;
(2)若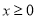 解关于
解关于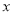 的不等式
的不等式
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
一个样本容量为10的样本数据,它们组成一个公差不为O的等差数列{ },若a3 =8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是( )
},若a3 =8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是( )
A.13,12 B.13,13 C.12,13 D.13,14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com