
(1)求c的值.
(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由.
(3)求|AC|的取值范围.
(文)已知函数f(x)=x4-4x3+ax2-1在区间[0,1]单调递增,在区间[1,2)单调递减.
(1)求a的值;
(2)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(3)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理由.
(理)解:(1)f′(x)=3ax2+2bx+c.
依题意f(x)在[-1,0]和[0,2]上有相反的单调性.
所以x=0是f(x)的一个极值点.
故f′(0)=0,得c=0.
(2)令f′(x)=0,得3ax2+2bx=0.
解得x1=0,x2=![]() .
.
因为f(x)在[0,2]和[4,5]上有相反的单调性,
所以f′(x)在[0,2]和[4,5]上有相反的符号.
故2≤![]() ≤4
≤4![]() -6≤
-6≤![]() ≤-3.
≤-3.
假设存在点M(x0,y0)使得f(x)在点M处的切线斜率为3b,则f′(x0)=3b,
即3ax02+2bx0-3b=0.
因为Δ=(2b)2-4×3a(-3b)=4b2+36ab=4ab(![]() +9),
+9),
且-6≤![]() ≤-3,所以3≤
≤-3,所以3≤![]() +9≤6,且a、b异号.
+9≤6,且a、b异号.
所以Δ=4ab(![]() +9)<0.
+9)<0.
故不存在点M(x0,y0),使得f(x)在点M处的切线斜率为3b.
(3)设A(α,0),C(β,0),依题意可令f(x)=a(x-α)(x-2)(x-β),
即f(x)=a[x3-(2+α+β)x2+(2α+2β+αβ)x-2αβ]
=ax3-a(2+α+β)x2+a(2α+2β+αβ)x-2aαβ.
所以![]()
即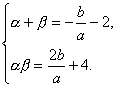 .
.
所以|AC|=|α-β|=![]() .
.
因为-6≤![]() ≤-3,所以当
≤-3,所以当![]() =-6时,|AC|max=
=-6时,|AC|max=![]() ;
;
当![]() =-3时,|AC|min=3.
=-3时,|AC|min=3.
故3≤|AC|≤4![]() .
.
(文)解:(1)由函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2)上单调递减,所以x=1时,取得极大值.
所以f′(1)=0.
因为f′(x)=4x3-12x2+2ax,
所以4-12+2a=0.解得a=4.
(2)因为点A(x0,f(x0))关于直线x=1的对称点B的坐标为(2-x0,f(x0)),
且f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1
=(2-x0)2[(2-x0)-2]2-1
=x04-4x03+4x02-1=f(x0).
所以点A关于直线x=1的对称点B也在函数f(x)的图象上.
(3)因为函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,
等价于方程x4-4x3+4x2-1=bx2-1恰有3个不等实根.
由x4-4x3+4x2-1=bx2-1,得x4-4x3+(4-b)x2=0.
因为x=0是其中一个根,
所以方程x2-4x+(4-b)=0有2个非零且不等的实数根.
故由![]() 得b>0且b≠4.
得b>0且b≠4.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
| m |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样理)(14分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(![]() R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(Ⅰ)设![]() ,若h (x)为偶函数,求
,若h (x)为偶函数,求![]() ;
;
(Ⅱ)设![]() ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
(Ⅲ)试判断h(x)能否为任意的一个二次函数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中四模理) 已知f(x)=sin(x+![]() ), g(x)=cos(x-
), g(x)=cos(x-![]() ) ,则f(x)的图象
) ,则f(x)的图象
A.与g(x)的图象相同 B.与g(x)的图象关于y轴对称
C.向左平移![]() 个单位,得到g(x)的图象 D.向右平移
个单位,得到g(x)的图象 D.向右平移![]() 个单位,得到g(x)的图象
个单位,得到g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年福建卷理)(14分)
已知f(x)=![]() (x∈R)在区间[-1,1]上是增函数。
(x∈R)在区间[-1,1]上是增函数。
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=![]() 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com