
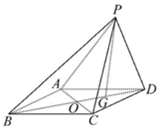
 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$. 分析 利用向量的三角形法则、平行四边形法则即可得出.
解答 解:$\overrightarrow{PG}$=$\overrightarrow{PB}$+$\overrightarrow{BG}$=$\overrightarrow{PB}$+$\frac{2}{3}$$\overrightarrow{BD}$=$\overrightarrow{PB}$+$\frac{2}{3}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\overrightarrow{PB}$+$\frac{2}{3}$($\overrightarrow{PA}$-$\overrightarrow{PB}$+$\overrightarrow{PC}$-$\overrightarrow{PB}$)=$\frac{2}{3}$$\overrightarrow{PA}$-$\frac{1}{3}$$\overrightarrow{PB}$+$\frac{2}{3}$$\overrightarrow{PC}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$,
而$\overrightarrow{PB}$=$\overrightarrow{PG}$+$\overrightarrow{GB}$,
故$\overrightarrow{BG}$=$\overrightarrow{PG}$-$\overrightarrow{PB}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$-$\overrightarrow{b}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$,
故答案为:$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
点评 本题考查了向量的三角形法则、平行四边形法则及其运算性质,考查了推理能力与计算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:选择题
为了得到函数y=sin(2x-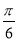 )的图象,可以将函数y=cos 2x的图象 ( )
)的图象,可以将函数y=cos 2x的图象 ( )
A.向右平移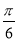 个单位长度
个单位长度
B.向右平移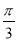 个单位长度
个单位长度
C.向左平移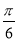 个单位长度
个单位长度
D.向左平移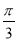 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
设奇函数f(x)在(0,+∞)上是增函数,且f(1)=0,则不等式x[f(x)-f(-x)]<0的解集为 ( )
A.{x|-1<x<0或x>1} B.{x|x<-1或0<x<1}
C.{x|x<-1或x>1} D.{x|-1<x<0或0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a<0时,f(x)有两个零点 | B. | 当a=0时,f(x)无零点 | ||
| C. | 当0<a<1时,f(x)有小于1的零点 | D. | 当a>1时,f(x)有大于a的零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com