已知向量$\overrightarrow{a}$=(m.1).$\overrightarrow{b}$=.若$\overrightarrow{a}∥\overrightarrow{b}$.则2m+n=1．题目和参考答案——青夏教育精英家教网—

16．已知向量$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（1-n，2），若$\overrightarrow{a}∥\overrightarrow{b}$，则2m+n=1．

分析根据题意，由向量平行的坐标表示公式可得若$\overrightarrow{a}∥\overrightarrow{b}$，则有2×m=1×（1-n），变形可得2m+n=1；即可得答案．

解答解：根据题意，向量$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（1-n，2），
若$\overrightarrow{a}∥\overrightarrow{b}$，则有2×m=1×（1-n），即2m=1-n，
变形可得2m+n=1；
故答案为：1．

点评本题考查向量平行的坐标运算，关键掌握向量平行的坐标表示公式．

练习册系列答案

浙江新中考系列答案

68所名校图书小学毕业升学必备系列答案

天利38套新课标全国中考试题精选系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2015-2016学年河南省商丘市高一文下学期期末考数学试卷（解析版） 题型：解答题

随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图所示．

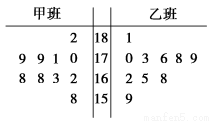
（Ⅰ）根据茎叶图判断哪个班的平均身高较高；

（Ⅱ）计算甲班的样本方差；

（Ⅲ）现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学求身高为176 cm的同学被抽中的概率．

查看答案和解析>>

科目：高中数学 来源：2015-2016学年河南省商丘市高一理下学期期末考数学试卷（解析版） 题型：选择题

执行如图所示的程序框图，如果输入的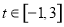，则输出的s属于（）

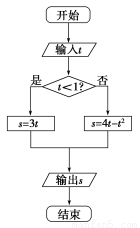
A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5]

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

4．解方程1+4+7+10+…+x=117，得x=25．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．求函数y=2a$\sqrt{x}$-$\frac{1}{x}$在x∈（0，1]上的最大值（其中a∈R）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

1．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞b＞0）$左右焦点分别为F₁，F₂，过F₁做直线l与双曲线左右分别交于P，Q两点，若三角形PQF₂是以Q为直角的等腰直角三角形，则e²=（　　）

A．

$5-2\sqrt{2}$

B．

$5+2\sqrt{2}$

C．

$4+2\sqrt{2}$

D．

$4-2\sqrt{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．

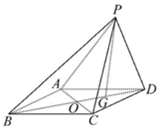四棱锥P-ABCD中，四边形ABCD为平行四边形，AC与BD交于点O，点G为BD上一点，BG=2GD，$\overrightarrow{PA}$=$\overrightarrow{a}$，$\overrightarrow{PB}$=$\overrightarrow{b}$，$\overrightarrow{PC}$=$\overrightarrow{c}$，用基底{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．已知全集U={1，2，3，4，5，6}，集合P={1，3，5}，Q={1，2，4}，则（∁_UP）∩Q=（　　）

A．

{1}

B．

{2，4}

C．

{2，4，6}

D．

{1，2，4，6}

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

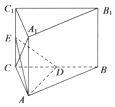已知三棱柱ABC-A₁B₁C₁的底面是边长为4的正三角形，侧棱AA₁垂直于底面ABC，AA₁=2$\sqrt{2}$，D为BC中点．
（Ⅰ）若E为棱CC₁的中点，求证：A₁C⊥DE；
（Ⅱ）若点E在棱CC₁上，直线CE与平面ADE所成角为α，当sinα=$\frac{2\sqrt{5}}{5}$时，求CE的长．

查看答案和解析>>

同步练习册答案