
| A. | $5-2\sqrt{2}$ | B. | $5+2\sqrt{2}$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
分析 设|QF2|=|PQ|=m,计算出|PF2|=$\sqrt{2}$m,运用双曲线的定义,再利用勾股定理,即可建立a,c的关系,从而求出e2的值.
解答 解:设|QF2|=|PQ|=m,
则|PF2|=$\sqrt{2}$m,
由双曲线的定义可得|QF1|=m+2a,|PF1|=$\sqrt{2}$m-2a,
∵|PQ|=|QF1|-|PF1|=m,
∴m+2a-($\sqrt{2}$m-2a)=m,
∴4a=$\sqrt{2}$m,即m=2$\sqrt{2}$a,
∵△QF1F2为直角三角形,
∴|F1F2|2=|QF1|2+|QF2|2
∴4c2=(2+2$\sqrt{2}$)2a2+(2$\sqrt{2}$a)2,
∴4c2=(20+8$\sqrt{2}$)a2,
由e=$\frac{c}{a}$可得
e2=5+2$\sqrt{2}$.
故选:B.
点评 本题考查双曲线的标准方程与性质:离心率,考查双曲线的定义,利用勾股定理求解,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:填空题
O是面α上一定点,A,B,C是面α上△ABC的三个顶点,∠B,∠C分别是边AC,AB的对角.以下命题正确的是________.(把你认为正确的序号全部写上)
①动点P满足 ,则△ABC的外心一定在满足条件的P点集合中;
,则△ABC的外心一定在满足条件的P点集合中;
②动点P满足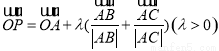 ,则△ABC的内心一定在满足条件的P点集合中;
,则△ABC的内心一定在满足条件的P点集合中;
③动点P满足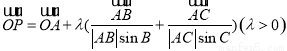 ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;
④动点P满足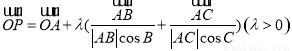 ,则△ABC的垂心一定在满足条件的P点集合中.
,则△ABC的垂心一定在满足条件的P点集合中.
⑤动点P满足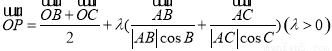 ,则△ABC的外心一定在满足条件的P点集合中.
,则△ABC的外心一定在满足条件的P点集合中.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
通常表明地震能量大小的尺度是里氏震级,其计算公式为: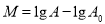 ,其中,
,其中,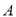 是被测地震的最大振幅,
是被测地震的最大振幅,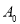 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是30,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算8级地震的最大振幅是5级地震的最大振幅的多少倍?
(以下数据供参考: ,
, 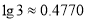 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a<0时,f(x)有两个零点 | B. | 当a=0时,f(x)无零点 | ||
| C. | 当0<a<1时,f(x)有小于1的零点 | D. | 当a>1时,f(x)有大于a的零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com