考点:用空间向量求平面间的夹角,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)由已知可取正三角形ABC的边BC的中点O,得到AO⊥平面BCC
1B
1.取B
1C
1中点O
1,以O为原点,
,
,
的方向为x,y,z轴的正方向建立空间直角坐标系,
求出平面A
1BD内的两个向量的坐标,由数量积为0得到向量垂直,进一步得到线线垂直,则线面垂直;
(2)设出平面A
1AD的法向量,由数量积为0求解该法向量,结合(Ⅰ)可知
为平面A
1BD的法向量,然后直接由两向量所成角的余弦值得二面角A-A
1D-B的余弦值;
(3)直接由向量求点到平面的距离公式得答案.
解答:
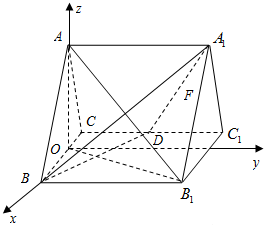
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,
∴AO⊥BC.
∵在正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,
∴AO⊥平面BCC
1B
1.
取B
1C
1中点O
1,以O为原点,
,
,
的方向为x,y,z轴的正方向建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),
A1(0,2,),
A(0,0,),B
1(1,2,0),
∴
=(1,2,-),
=(-2,1,0),
=(-1,2,).
∵
•=-2+2+0=0,
•=-1+4-3=0,
∴
⊥,
⊥.
∴AB
1⊥平面A
1BD;
(Ⅱ)解:设平面A
1AD的法向量为
=(x,y,z).
=(-1,1,-),
=(0,2,0).
∵
n⊥,
n⊥,
∴
,
∴
,
∴
.
令z=1得平面A
1AD的一个法向量
=(-,0,1).
由(Ⅰ)知AB
1⊥平面A
1BD,
∴
为平面A
1BD的法向量.
cos<n,
>===-.
∴二面角A-A
1D-B的大小为θ,
∴
cosθ=;
(Ⅲ)解:由(Ⅱ)知,
为平面A
1BD法向量,
∵
=(-2,0,0),=(1,2,-).
∴点C到平面A
1BD的距离
d===.
点评:本题考查了空间直线与平面垂直的判断,考查了空间中点到平面的距离计算,训练了利用向量求解空间角和距离问题,是中档题.

 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案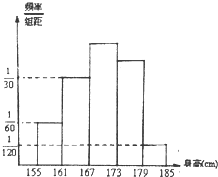 某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )
某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )