
分析 (1)由题意可得f(x)=-f(x+2)=-(-f(x+4))=f(x+4);
(2)由[0,2]上的表达式先求[-2,0]上的表达式,再求[2,4]上的表达式;
(3)由周期性可化为f(0)+f(1)+f(2)+…+f(2015)=504[f(0)+f(1)+f(2)+f(-1)],再由奇偶性求解.
解答 (1)证明:∵f(x+2)=-f(x),
∴f(x)=-f(x+2)=-(-f(x+4))=f(x+4);
(2)解:∵当x∈[0,2]时,f(x)=2x-x2,
又∵f(x)是定义在R上的奇函数,
∴x∈[-2,0]时,f(x)=2x+x2,
故当x∈[2,4]时,f(x)=f(x-4)
=2(x-4)+(x-4)2
=x2-6x+8;
(3)解:∵f(x+4)=f(x),
∴f(x)是以4为周期的周期函数;
∴f(0)+f(1)+f(2)+…+f(2015)
=504[f(0)+f(1)+f(2)+f(3)]
=504[f(0)+f(1)+f(2)+f(-1)]
=0.
点评 本题考查了抽象函数的周期性与奇偶性的判断与应用,同时考查了函数解析式的求法,属于中档题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
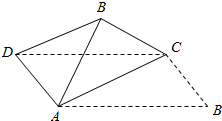 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
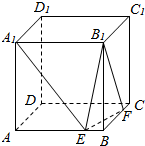 如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.
如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com