练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若f(x)＝，e<a<b，则                                           (　　)

    A．f(a)>f(b)                       B．f(a)＝f(b)

    C．f(a)<f(b)                       D．f(a)f(b)>1

    A

    解析　f′(x)＝，当x>e时，f′(x)<0，

    则f(x)在(e，＋∞)上为减函数，f(a)>f(b)，故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、理科数学(福建卷) 题型：013

    对于具有相同定义域D的函数f(x)和g(x)，若存在函数h(x)＝kx＋b(k，b为常数)，对任给的正数m，存在相应的x0∈D，使得当x∈D且x＞x0时，总有则称直线l：y＝kx＋b为曲线y＝f(x)与y＝g(x)的“分渐近线”．给出定义域均为D＝{x|x＞1}的四组函数如下：

    ①f(x)＝x2，g(x)＝；

    ②f(x)＝10－x＋2，g(x)＝；

    ③f(x)＝，g(x)＝；

    ④f(x)＝，g(x)＝2(x－1－e－x)

    其中，曲线y＝f(x)与y＝g(x)存在“分渐近线”的是

    [　　]
    A．

    ①④

    B．

    ②③

    C．

    ②④

    D．

    ③④

    查看答案和解析>>

    科目：高中数学 来源：山西省忻州一中2010届高三第三次四校联考数学理科试题 题型：044

    设函数h(x)＝x2，(x)＝2elnx(e为自然对数的底)．

    (1)求函数F(x)＝h(x)－x的极值；

    (2)若存在常数k和b，使得函数f(x)和g(x)对其定义域内的任意实数x分别满足f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为函数f(x)和g(x)的“隔离直线”．试问：函数h(x)和(x)是否存在“隔离直线”？若存在，求出“隔离直线”方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌一中、南昌十中2011届高三第一次联考理科数学试题 题型：044

    已知函数f(x)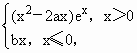＝g(x)＝clnx＋b，且x＝是函数y＝f(x)的极值点．

    (Ⅰ)求实数a的值；

    (Ⅱ)若方程f(x)－m＝0有两个不相等的实数根，求实数m的取值范围；

    (Ⅲ)若直线l是函数y＝f(x)的图象在点(2，f(2))处的切线，且直线l与函数y＝g(x)的图象相切于点P(x0，y0)，x0∈[e－1，e]，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：江西省重点中学协作体2012届高三第一次联考数学理科试题 题型：044

    已知函数f(x)＝ax－lnx＋1(a∈R)，g(x)＝xe1－x．

    (Ⅰ)求函数g(x)在区间(0，e]上的值域；

    (Ⅱ)是否存在实数a，对任意给定的x0∈(0，e]，在区间[1，e]上都存在两个不同的xi(i＝1，2)，使得f(xi)＝g(x0)成立．若存在，求出a的取值范围；若不存在，请说明理由；

    (Ⅲ)给出如下定义：对于函数y＝F(x)图象上任意不同的两点A(x1，y1)，B(x2，my2)，如果对于函数y＝F(x)图象上的点M(x0，y0)(其中总能使得F(x1)－f(x2)＝(x0)(x1－x2)成立，则称函数具备性质“L”，试判断函数f(x)是不是具备性质“L”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：重庆市重庆一中2012届高三9月月考数学理科试题 题型：044

    若存在实数k和b，使得函数f(x)与g(x)对其定义域上的任意实数x分别满足：f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为f(x)与g(x)的“和谐直线”．已知h(x)＝x2，(x)＝2elnx，(e为自然对数的底数)；

    (1)求F(x)＝h(x)－(x)的极值；

    (2)函数h(x)和(x)是否存在和谐直线？若存在，求出此和谐直线方程；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案