
| A�� | $\frac{31}{5}$ | B�� | $\frac{32}{5}$ | C�� | 6 | D�� | 7 |
���� ����֪���õȲ����е�ͨ�ʽ�����$\frac{{a}_{2}+{a}_{5}+{a}_{17}+{a}_{22}}{{b}_{8}+{b}_{10}+{b}_{12}+{b}_{16}}$=$\frac{{a}_{1}+{a}_{22}}{{b}_{1}+{b}_{22}}$�����ɵȲ�����ǰn���ʽ�Ƶ���ԭʽ����$\frac{{S}_{22}}{{T}_{22}}$���ɴ������������
��� �⣺�ߵȲ�����{an}��{bn} ��ǰn���S�ֱ�ΪSn��Tn����$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+1}{n+3}$��
���ɵȲ����е�ͨ�ʽ�ɵã�
$\frac{{a}_{2}+{a}_{5}+{a}_{17}+{a}_{22}}{{b}_{8}+{b}_{10}+{b}_{12}+{b}_{16}}$
=$\frac{2��2{a}_{1}+21d��}{2��2{b}_{1}+21d��}$
=$\frac{{a}_{1}+{a}_{22}}{{b}_{1}+{b}_{22}}$
=$\frac{\frac{22��{a}_{1}+{a}_{22}��}{2}}{\frac{22��{b}_{1}+{b}_{22}��}{2}}$
=$\frac{{S}_{22}}{{T}_{22}}$=$\frac{7��22+1}{22+3}$
=$\frac{155}{25}$=$\frac{31}{5}$��
��ѡ��A��
���� ���⿼�������Ȳ����е�������ĺ͵ı�ֵ�������е��⣬����ʱҪ�������⣬ע��Ȳ����е����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
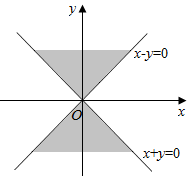 ������������ʽ����x2-y2��0����x2-y2��0����x2+y2��0����ͼ��ʾ����Ӱ����Ӧ�����Ϊ�ڵIJ���ʽ����ʾ��ƽ������
������������ʽ����x2-y2��0����x2-y2��0����x2+y2��0����ͼ��ʾ����Ӱ����Ӧ�����Ϊ�ڵIJ���ʽ����ʾ��ƽ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 60�� | C�� | 60���120�� | D�� | 30���150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com