Question

1．如图，在边长为2的菱形ABCD中，∠BAD=60°，现将△ABD沿BD翻折至△A′BD，使二面角A′-BD-C的大小为60°，求CD和平面A′BD所成角的余弦值是$\frac{{\sqrt{7}}}{4}$．

Answer 1

分析 根据条件先判断∠A′OC是二面角A′-BD-C的平面角，从而△A′OC为等边三角形，根据线面所成角的定义得到∠CDE是CD和平面A′BD所成的角，根据三角形的边角关系进行求解即可．

解答 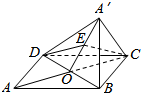解：连接AC交B于O，连接OA′，
∵ABCD是菱形，
∴OC⊥BD，A′O⊥BC，
即∠A′OC是二面角A′-BD-C的平面角，
即∠A′OC=60°，
连接A′C，则△A′OC为等边三角形，
则平面A′OC⊥平面ABCD，
取A′O的中点E，连接CE，
则CE⊥A′O，且CE⊥平面A′BD，
连接DE，则∠CDE是CD和平面A′BD所成的角，
∵在边长为2的菱形ABCD中，∠BAD=60°，
∴BD=6，AO=OC=A′O=$\sqrt{3}$，
则OE=$\frac{1}{2}A′O=\frac{\sqrt{3}}{2}$，OD=1，
则DE=$\sqrt{{1}^{2}+（\frac{\sqrt{3}}{2}）^{2}}$=$\frac{\sqrt{7}}{2}$，
则cos∠CDE=$\frac{DE}{CD}=\frac{\frac{\sqrt{7}}{2}}{2}$=$\frac{{\sqrt{7}}}{4}$，
故答案为：$\frac{{\sqrt{7}}}{4}$

点评 本题主要考查空间二面角和直线和平面所成角的应用，根据空间角的定义寻找二面角和直线和平面所成的角是解决本题的关键．