
五位同学各自制作了一张贺卡,分别装入5个空白信封内,这五位同学每人随机地抽取一封,则恰好有两人抽取到的贺卡是其本人制作的概率是 .
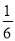
【解析】
试题分析:根据题意,首先由排列数公式分析可得5位同学每人随机地抽取1张卡片的情况;进而分两步分析5人中恰好有2人抽取到的贺卡是其本人制作的情况数目,①先在5人中抽出2人,使其抽取到的贺卡是其本人制作的,②分析抽到的都不是其本人制作的3人,由分步计数原理可得其情况数目,由等可能事件的概率公式,计算可得答案.
根据题意,共5张贺卡,5位同学每人随机地抽取1张,有A55=120种情况,要满足5人中恰好有2人抽取到的贺卡是其本人制作,可以先在5人中抽出2人,使其抽取到的贺卡是其本人制作的,有C52=10种情况,则剩余的3人,抽到的都不是其本人制作的,有2种情况,则5人中恰好有2人抽取到的贺卡是其本人制作的情况有10×2=20种,
其概率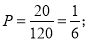
考点:等可能事件的概率.


科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:解答题
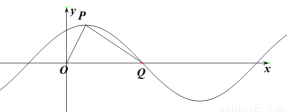
(本题满分12分)已知函数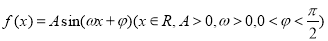 的部分图象如图所示,
的部分图象如图所示,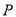 是图象的最高点,
是图象的最高点,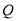 为图象与
为图象与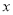 轴的交点,
轴的交点,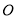 为坐标原点,若
为坐标原点,若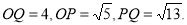
(1)求函数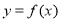 的解析式,
的解析式,
(2)将函数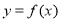 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数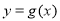 的图象,当
的图象,当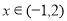 时,求函数
时,求函数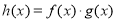 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:解答题
对于给定数列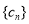 ,如果存在实常数
,如果存在实常数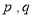 使得
使得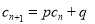 对于任意
对于任意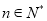 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
,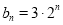 ,
,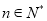 ,数列
,数列 、
、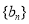 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:选择题
若正数a,b,c成公差不为零的等差数列,则 ( )
(A)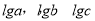 成等差数列
成等差数列
(B)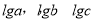 成等比数列
成等比数列
(C)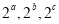 成等差数列
成等差数列
(D)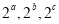 成等比数列
成等比数列
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测理科数学试卷(解析版) 题型:解答题
已知函数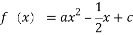 (
(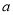 、
、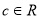 ),满足
),满足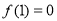 ,且
,且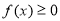 在
在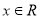 时恒成立.
时恒成立.
(1)求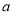 、
、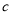 的值;
的值;
(2)若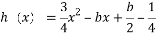 ,解不等式
,解不等式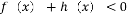 ;
;
(3)是否存在实数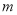 ,使函数
,使函数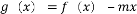 在区间
在区间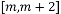 上有最小值
上有最小值 ?若存在,请求出
?若存在,请求出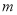 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知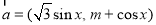 ,
,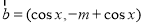 , 且
, 且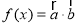 .
.
(1)求函数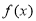 的周期;
的周期;
(2)当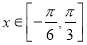 时,
时, 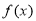 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 及相应的
的最大值, 及相应的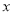 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com