
分析 (Ⅰ)分两类,选0或不选0,分类加法计数原理可得,
(Ⅱ)分两类,个位和十位有选到0或个位和十位没有选到0,分类加法计数原理可得.
解答 解:(Ⅰ)第一类,不选到0,则共有$A_5^5=5×4×3×2×1=120$个;
第二类,若选到0,则共有C54A41A44=480个
由分类加法计数原理,共可以组成120+480=600个无重复数字的五位数字.
(Ⅱ)第一类,个位和十位有选到0,则共有$C_2^1A_2^2A_4^2=2×2×1×4×3=48$个
第二类,个位和十位没有选到0,则共有$A_2^2A_3^1A_3^1=2×1×3×3=18$个
由分类加法计数原理,共可以组成48+18=66个.
点评 本题考查了分类计数原理,关键是分类,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
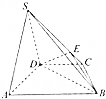 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,AB∥DC,△SAD是等边三角形,且SD=2,BD=2$\sqrt{3}$,AB=2CD=4.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,AB∥DC,△SAD是等边三角形,且SD=2,BD=2$\sqrt{3}$,AB=2CD=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
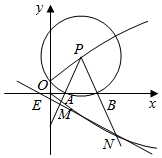 已知点F是抛物线C:y2=4x的焦点,P是抛物线C在第一象限内的点,且|PF|=5.
已知点F是抛物线C:y2=4x的焦点,P是抛物线C在第一象限内的点,且|PF|=5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>-2 | B. | m>-4 | C. | m<-2 | D. | m<-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-8 b=-10 | B. | a=-4 b=-9 | C. | a=-1 b=9 | D. | a=-1 b=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
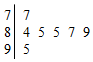
| A. | 86,86 | B. | 85,84 | C. | 84,86 | D. | 86,85 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com