
���� ��1����l�ķ���Ϊy=1ʱ��ֱ��l����Բ���У��õ�b=1��������Բ��������Ϊ$\frac{\sqrt{2}}{2}$����a=$\sqrt{2}$���ɴ��������Բ�ı����̣�
��2����ֱ��l����Բ���У��ã�km+$\sqrt{2}$��2=1+k2����$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx+\sqrt{2}}\end{array}\right.$���ã�1+2k2��x2+4$\sqrt{2}kx+2=0$���ɴ����ø����б�ʽ��Τ�ﶨ��������������������Բ�ҳ���ʽ�������֪���������������${y}^{2}=-2\sqrt{2}x$��ԲM�������������̾��룮
��� �⣺��1����ԲM����x-m��2+y2=1������l����l�ķ���Ϊy=1ʱ��ֱ��l����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����У�
��b=1��
����Բ��������Ϊ$\frac{\sqrt{2}}{2}$����e=$\frac{c}{a}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$�����a=$\sqrt{2}$��
����Բ�ı�����Ϊ$\frac{{{x}^{2}}_{\;}}{2}$+y2=1��
��2����ֱ��l����Բ���У���$\frac{|km+\sqrt{2}|}{\sqrt{1+{k}^{2}}}$=1��
�ࣨkm+$\sqrt{2}$��2=1+k2��
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx+\sqrt{2}}\end{array}\right.$���ã�1+2k2��x2+4$\sqrt{2}kx+2=0$��
��P��x1��y1����Q��x2��y2������$��=��4\sqrt{2}k��^{2}-8��1+2{k}^{2}����0$�����${k}^{2}��\frac{1}{2}$��
��${x}_{1}+{x}_{2}=\frac{-4\sqrt{2}k}{1+2{k}^{2}}$��${x}_{1}{x}_{2}=\frac{2}{1+2{k}^{2}}$��
��${y}_{1}{y}_{2}=��k{x}_{1}+\sqrt{2}����k{x}_{2}+\sqrt{2}��$=${k}^{2}{x}_{1}{x}_{2}+\sqrt{2}k��{x}_{1}+{x}_{2}��+2$=$\frac{2-2{k}^{2}}{1+2{k}^{2}}$��
��tan��POQ=3S��POQ����tan$��POQ=3��\frac{1}{2}|\overrightarrow{OP}|•|\overrightarrow{OQ}|$sin��POQ��
��$|\overrightarrow{OP}|•|\overrightarrow{OQ}|$cos��POQ=$\overrightarrow{OP}•\overrightarrow{OQ}$=$\frac{2}{3}$��
��$\overrightarrow{OP}•\overrightarrow{OQ}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}$=$\frac{4-2{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{3}$����${k}^{2}=1��\frac{1}{2}$��
�ࣨkm+$\sqrt{2}$��2=2����m=0���ᣩ����m=2$\sqrt{2}$���ᣩ��m=-2$\sqrt{2}$��
��ԲM����x+2$\sqrt{2}$��2+y2=1��
��������${y}^{2}=-2\sqrt{2}x$��һ��P��x��y����
��|PM|=$\sqrt{��x+2\sqrt{2}��^{2}+{y}^{2}}$=$\sqrt{��x+2\sqrt{2}��^{2}-2\sqrt{2}x}$=$\sqrt{��x+\sqrt{2}��^{2}+6}$��
��x=-$\sqrt{2}$ʱ��|PM|����Сֵ$\sqrt{6}$��1��
��������y2=2$\sqrt{2}x$��|PM|����Сֵ$\sqrt{6}��1$��
��������${y}^{2}=-2\sqrt{2}x$��ԲM�������������̾��뼴|AB|����СֵΪ$\sqrt{6}-1$��
���� ���⿼����Բ���̵��������߶γ�����Сֵ�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ��������������������Բ�ҳ���ʽ����Բ��Բ�������ߵ�֪ʶ��ĺ������ã�


 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
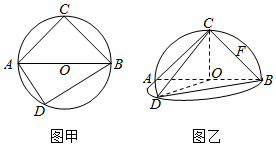 ��ͼ�ף���O��ֱ��AB=2��Բ������C��D��ֱ��AB�����࣬ʹ��CAB=$\frac{��}{4}$����DAB=$\frac{��}{3}$����ֱ��AB����ʹ������Բ���ڵ�ƽ�滥�ഹֱ����ͼ�ң���FΪBC���е㣬����ͼ�ҽ�����и��⣺
��ͼ�ף���O��ֱ��AB=2��Բ������C��D��ֱ��AB�����࣬ʹ��CAB=$\frac{��}{4}$����DAB=$\frac{��}{3}$����ֱ��AB����ʹ������Բ���ڵ�ƽ�滥�ഹֱ����ͼ�ң���FΪBC���е㣬����ͼ�ҽ�����и��⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������ABCD-A1B1C1D1����EΪ��AA1���е㣬������ֱ��B1D1��DE���ɽǵĴ�С��arccos$\frac{\sqrt{10}}{5}$������÷����Ǻ���ֵ��ʾ��
��֪������ABCD-A1B1C1D1����EΪ��AA1���е㣬������ֱ��B1D1��DE���ɽǵĴ�С��arccos$\frac{\sqrt{10}}{5}$������÷����Ǻ���ֵ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC��BC��AC��BC=AC=2��AA1=3��DΪAC���е�
��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC��BC��AC��BC=AC=2��AA1=3��DΪAC���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
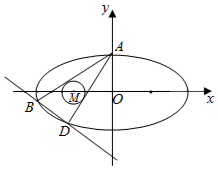 ��ͼ����֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���϶���ΪA��0��1����������Ϊ$\frac{{\sqrt{3}}}{2}$��
��ͼ����֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���϶���ΪA��0��1����������Ϊ$\frac{{\sqrt{3}}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
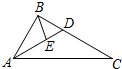 ��ͼ���ڡ�ABC�У���֪$��BAC=\frac{��}{3}$��AB=2��AC=4����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����BE=$\frac{2\sqrt{21}}{9}$��
��ͼ���ڡ�ABC�У���֪$��BAC=\frac{��}{3}$��AB=2��AC=4����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����BE=$\frac{2\sqrt{21}}{9}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com