
【题目】抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点.
两点.
(1)![]() 为坐标原点,求证:
为坐标原点,求证:![]() ;
;
(2)设点![]() 在线段
在线段![]() 上运动,原点
上运动,原点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,求四边形
,求四边形![]() 面积的最小值
面积的最小值
【答案】(Ⅰ)见解析;(Ⅱ)![]() 时,四边形
时,四边形![]() 的面积最小,最小值是
的面积最小,最小值是![]() .
.
【解析】
试题(1)先利用已知条件设出直线AB的方程,与抛物线联立方程组,然后结合韦达定理表示出向量的数量积,进而证明。
(2)根据由点![]() 与原点
与原点![]() 关于点
关于点![]() 对称,得
对称,得![]() 是线段
是线段![]() 的中点,从而点
的中点,从而点![]() 与点
与点![]() 到直线
到直线![]() 的距离相等,得到四边形
的距离相等,得到四边形![]() 的面积等于
的面积等于![]() ,结合三角形面积公式得到。
,结合三角形面积公式得到。
(Ⅰ)解:依题意![]() ,设直线
,设直线![]() 方程为
方程为![]() . …………1分
. …………1分
将直线![]() 的方程与抛物线的方程联立,消去
的方程与抛物线的方程联立,消去![]() 得
得![]() .……3分
.……3分
设![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
![]() =1,
=1,
故![]() .………………6分
.………………6分
(Ⅱ)解:由点![]() 与原点
与原点![]() 关于点
关于点![]() 对称,得
对称,得![]() 是线段
是线段![]() 的中点,从而点
的中点,从而点![]() 与点
与点![]() 到直线
到直线![]() 的距离相等,所以四边形
的距离相等,所以四边形![]() 的面积等于
的面积等于![]() .……8分
.……8分
因为![]() ……………9分
……………9分
![]() ,…………11分
,…………11分
所以![]() 时,四边形
时,四边形![]() 的面积最小,最小值是
的面积最小,最小值是![]() . ……12分
. ……12分


科目:高中数学 来源: 题型:
【题目】有一款击鼓小游戏规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得50分,没有出现音乐则扣除150分(即获得-150分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(Ⅰ)玩一盘游戏,至少出现一次音乐的概率是多少?
(Ⅱ)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)许多玩过这款游戏的人都发现,玩的盘数越多,分数没有增加反而减少了.请运用概率统计的相关知识分析其中的道理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)关于![]() 的不等式
的不等式![]() 的解集为一切实数,求实数
的解集为一切实数,求实数![]() 的取值范围;
的取值范围;
(3)关于![]() 的不等式
的不等式![]() 的解集中的正整数解恰有
的解集中的正整数解恰有![]() 个,求实数
个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为a的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为![]() .
.
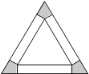
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的水轮绕着圆心
的水轮绕着圆心![]() 逆时针做匀速圆周运动,每分钟转动
逆时针做匀速圆周运动,每分钟转动![]() 圈,水轮圆心
圈,水轮圆心![]() 距离水面
距离水面![]() ,如果当水轮上点
,如果当水轮上点![]() 从离开水面的时刻(
从离开水面的时刻(![]() )开始计算时间.
)开始计算时间.
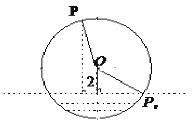
(1)试建立适当的平面直角坐标系,求点![]() 距离水面的高度
距离水面的高度![]() (
(![]() )与时间
)与时间![]() (
(![]() )满足的函数关系;
)满足的函数关系;
(2)求点![]() 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com