
 ;
;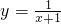 .
. 的图象可由函数y=
的图象可由函数y= 向右平移1个单位得到,故函数在区间(-∞,1)上单调递减,当然在(-∞,0)内单调递减;
向右平移1个单位得到,故函数在区间(-∞,1)上单调递减,当然在(-∞,0)内单调递减; 轴对称,故在(-∞,
轴对称,故在(-∞, )内单调递减,不能保证在(-∞,0)内单调递减;
)内单调递减,不能保证在(-∞,0)内单调递减;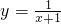 的图象可由函数y=
的图象可由函数y= 向左平移1个单位得到,故函数在区间(-∞,-1)上单调递减,不能保证在(-∞,0)内单调递减.
向左平移1个单位得到,故函数在区间(-∞,-1)上单调递减,不能保证在(-∞,0)内单调递减. 在(-∞,0)内单调递减;(2)y=1-x2在(-∞,0)内单调递增;(3)(4)均不能保证在(-∞,0)内单调递减
在(-∞,0)内单调递减;(2)y=1-x2在(-∞,0)内单调递增;(3)(4)均不能保证在(-∞,0)内单调递减

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com