
已知各顶点都在同一个球面上的正四棱锥高为3,体积为6,则这个球的表面积是_____.
科目:高中数学 来源: 题型:填空题
正三棱锥P—ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B—PA—C大小的取值范围是( ,π);
,π);
②若MN⊥AM,则PC与平面PAB所成角的大小为 ;
;
③过点M与异面直线PA和BC都成 的直线有3条;
的直线有3条;
④若二面角B—PA—C大小为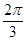 ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成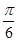 的直线有3条.
的直线有3条.
正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=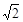 ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .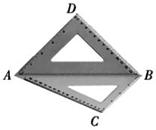
①当平面ABD⊥平面ABC时,C、D两点间的距离为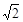 ;
;
②在三角板ABD转动过程中,总有AB⊥CD;
③在三角板ABD转动过程中,三棱锥D-ABC体积的最大值为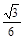 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com