
分析 设x$\overrightarrow{MN}$=$\overrightarrow{MA}$,函数f(x)的最小值化为点P到直线MN的距离,结合图形求出tmax=3时MN的长度.
解答 解:设x$\overrightarrow{MN}$=$\overrightarrow{MA}$,
则函数f(x)=|$\overrightarrow{MP}$-x$\overrightarrow{MN}$|=|$\overrightarrow{MP}$-$\overrightarrow{MA}$|=|$\overrightarrow{AP}$|,其中P为单位圆O上的点,
∵x$\overrightarrow{MN}$=$\overrightarrow{MA}$,
∴点A在直线MN上;
∴函数f(x)的最小值t为点P到直线MN的距离,
当tmax=3时,如图所示;
线段MN的长度为|MN|=2$\sqrt{{4}^{2}-(3-1)^{2}}$=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了向量知识的运用问题,也考查了转化思想与数形结合的应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m?α,n?α,n⊥l,则l⊥α | ||
| C. | 若m∥α,n⊥β,α⊥β,则m∥n | D. | 若l⊥α,l⊥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
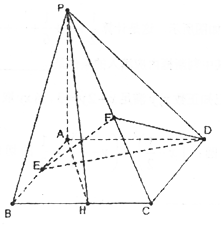 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
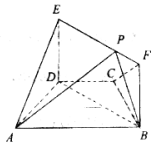 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2-x | B. | f(x)=x2 | C. | f(x)=3-x | D. | f(x)=cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com