【题目】 用总长14.8米的钢条制作一个长方体容器的框架，如果所制容器底面一边的长比另一边的长多0.5米，那么高为多少时容器的容积最大？最大容积是多少？
【答案】x=1时，即h=1.2时，V取到最大值1.8
【解析】本试题主要是考查了导数在实际生活中的运用。首先设出变量设底面一边长为x,则另一边长为x+0.5,高为h,容积为V，然后利用体积的公式表示出函数，结合导数的思想来判定单调性，确定出最值。
注意实际问题中，一个极值就是最值。
设底面一边长为x,则另一边长为x+0.5,高为h,容积为V
则4x+4(x+0.5)+4h=14.8,得到 h=3.2-2x
V=x(x+0.5)h =x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x (0<x<1.6)
由V’=0得x=1或
所以，x=1时，即h=1.2时，V取到最大值1.8
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】拖延症总是表现在各种小事上，但日积月累，特别影响个人发展.某校的一个社会实践调查小组，在对该校学生进行“是否有明显拖延症”的调查中，随机发放了110份问卷.对收回的100份有效问卷进行统计，得到如下
列联表：
（1）按女生是否有明显拖延症进行分层，已经从40份女生问卷中抽取了8份问卷，现从这8份问卷中再随机抽取3份，并记其中无明显拖延症的问卷的份数为
，试求随机变量
的分布列和数学期望；
（2）若在犯错误的概率不超过
的前提下认为无明显拖延症与性别有关，那么根据临界值表，最精确的
的值应为多少？请说明理由.附：独立性检验统计量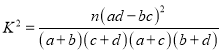
，其中
.
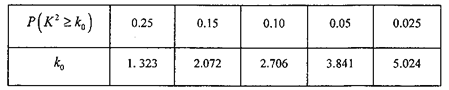
独立性检验临界值表：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两个班级均为40人，进行一门考试后，按学生考试成绩及 格与不及格进行统计，甲班及格人数为36人，乙班及格人数为24人．
(1) 根据以上数据建立一个
的列联表；
(2) 试判断成绩与班级是否有关？
参考公式：
，其中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足a1=1，an+1 
=1，记Sn=a12+a22+…+an2 ， 若S2n+1﹣Sn≤ 
对任意n∈N*恒成立，则正整数m的最小值是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知Sn是正项数列{an}的前n项和，且Sn= 
an2+ 
an﹣ 
（1）求数列{an}的通项公式；
（2）若an=2nbn ， 求数列{bn}的前n项和．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了得到函数y=sin（2x+ 
）的图象，只需将y=sin2x的图象上每一个点（ ）
A.横坐标向左平移 个单位
B.横坐标向右平移 个单位
C.横坐标向左平移 
个单位
D.横坐标向右平移 个单位
查看答案和解析>>
科目：高中数学 来源： 题型：
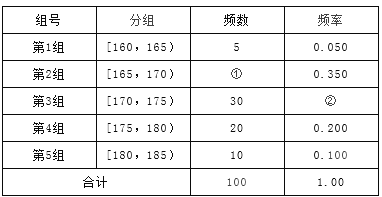
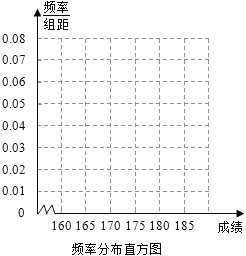
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下图所示．
（I）请先求出频率分布表中①、②位置相应数据，再在答题纸上完成下列频率分布直方图；
（Ⅱ）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（Ⅲ）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官的面试，求：第4组至少有一名学生被考官A面试的概率？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
