
如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点, ,
,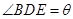 ,
,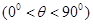 .
.
(1)当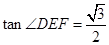 时,求
时,求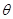 的大小;
的大小;
(2)求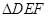 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时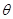 的值.
的值.
(1)θ=60°;(2)当θ=45°时,S取最小值 .
.
解析试题分析:本题主要考查正弦定理、直角三角形中正切的定义、两角和的正弦公式、倍角公式、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,在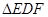 中,
中,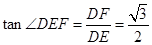 ,①,而在
,①,而在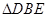 中,利用正弦定理,用
中,利用正弦定理,用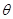 表示DE,在
表示DE,在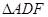 中,利用正弦定理,用
中,利用正弦定理,用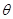 表示DF,代入到①式中,再利用两角和的正弦公式展开,解出
表示DF,代入到①式中,再利用两角和的正弦公式展开,解出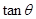 ,利用特殊角的三角函数值求角
,利用特殊角的三角函数值求角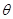 ;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.
;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.
在△BDE中,由正弦定理得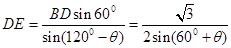 ,
,
在△ADF中,由正弦定理得 . 4分
. 4分
由tan∠DEF= ,得
,得 ,整理得
,整理得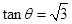 ,
,
所以θ=60°. 6分
(2)S= DE·DF=
DE·DF=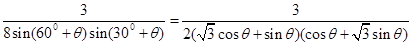
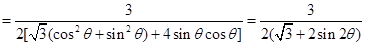 . 10分
. 10分
当θ=45°时,S取最小值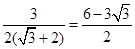 . 12分
. 12分
考点:正弦定理、直角三角形中正切的定义、两角和的正弦公式、倍角公式、三角形面积公式.


科目:高中数学 来源: 题型:解答题
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c= .
.
(1)若sinC=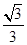 ,求sinA的值;
,求sinA的值;
(2)设f(C)= sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,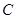 、
、 是两个小区所在地,
是两个小区所在地,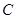 、
、 到一条公路
到一条公路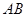 的垂直距离分别为
的垂直距离分别为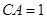
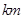 ,
,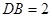
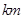 ,
,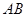 两端之间的距离为
两端之间的距离为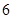
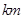 .
.
(1)某移动公司将在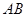 之间找一点
之间找一点 ,在
,在 处建造一个信号塔,使得
处建造一个信号塔,使得 对
对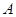 、
、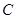 的张角与
的张角与 对
对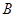 、
、 的张角相等,试确定点
的张角相等,试确定点 的位置.
的位置.
(2)环保部门将在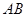 之间找一点
之间找一点 ,在
,在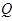 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得 对
对 、
、 所张角最大,试确定点
所张角最大,试确定点 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013·重庆高考)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+ ab.
ab.
(1)求A.
(2)设a= ,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com