
【题目】已知函数f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]() .
.
(1)求函数f(x)的单调减区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b= ![]() ,f(A﹣
,f(A﹣ ![]() )=
)= ![]() ,求角C.
,求角C.
【答案】
(1)解:f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]() =sin2x+
=sin2x+ ![]() cos2x=2sin(2x+
cos2x=2sin(2x+ ![]() ).
).
由2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,得x∈[kπ+
,得x∈[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z),
](k∈Z),
因此f(x)的单调递减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
(2)解:由f(A﹣ ![]() )=2sin[2(A﹣
)=2sin[2(A﹣ ![]() )+
)+ ![]() ]=2sin2A=
]=2sin2A= ![]() ,
,
又a<b,所以A为锐角,则A= ![]() .
.
由正弦定理得 ![]() sinB=
sinB= ![]() =
= ![]() ,
,
当B= ![]() 时,C=π﹣
时,C=π﹣ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
当B= ![]() 时,C=π﹣
时,C=π﹣ ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)根据二倍角公式及辅助角公式将f(x)化简,求得f(x)=2sin(2x+ ![]() ),根据正弦函数的单调性求得函数f(x)的单调减区间;(2)f(A﹣
),根据正弦函数的单调性求得函数f(x)的单调减区间;(2)f(A﹣ ![]() )=
)= ![]() ,代入(1)求得sin2A=
,代入(1)求得sin2A= ![]() ,由三角形的性质a<b,求得A,利用正弦定理求得sinB,分类讨论B的取值,分别求得角C.
,由三角形的性质a<b,求得A,利用正弦定理求得sinB,分类讨论B的取值,分别求得角C.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】设f(x)是连续的偶函数,且当x>0时,f(x)是单调函数,则满足f(x)=f( ![]() )的所有x之和为( )
)的所有x之和为( )
A.﹣4031
B.﹣4032
C.﹣4033
D.﹣4034
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:
(1)△ABC中平行于BC边的中位线所在直线的一般式方程和截距式方程;
(2)BC边的中线所在直线的一般式方程,并化为截距式方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,f(1))处的切线与x轴平行.
在点(1,f(1))处的切线与x轴平行.
(1)求实数a的值及f(x)的极值;
(2)若对任意x1 , x2∈[e2 , +∞),有| ![]() |>
|> ![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P(x,y)是曲线a|x|+b|y|=1(a≥0,b≥0)上任意一点,其坐标(x,y)均满足 ![]() ,则
,则 ![]() a+b取值范围为( )
a+b取值范围为( )
A.(0,2]
B.[1,2]
C.[1,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD,B1为PB的中点,D1为PD的中点,则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是( ) 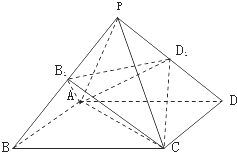
A.1:4
B.3:8
C.1:2
D.2:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com