
【题目】已知函数 ![]()
(1)求函数f(x)的定义域;
(2)求f(1)+f(﹣3)的值;
(3)求f(a+1)的值(其中a>﹣4且a≠1).
【答案】
(1)解:要使函数 ![]() 有意义
有意义
则 ![]()
即x≥﹣3且x≠2,
∴函数f(x)的定义域为{x|x≥﹣3且x≠2}(区间表示也可以)
(2)解:∵函数 ![]() ,
,
∴ ![]()
![]()
∴ ![]()
(3)解:∵函数 ![]() ,a>﹣4且a≠1,
,a>﹣4且a≠1,
∴f(a+1)= ![]() =
= ![]()
【解析】(1)要使函数 ![]() 有意义,则
有意义,则 ![]() ,由此能求出函数f(x)的定义域.(2)由函数
,由此能求出函数f(x)的定义域.(2)由函数 ![]() ,能求出f(1)+f(﹣3)的值.(3)由函数
,能求出f(1)+f(﹣3)的值.(3)由函数 ![]() ,能求出f(a+1)的值.
,能求出f(a+1)的值.
【考点精析】根据题目的已知条件,利用函数的定义域及其求法和函数的值的相关知识可以得到问题的答案,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知定义在(﹣1,1)上的函数f(x)满足:对任意x,y∈(﹣1,1)都有f(x)+f(y)=f(x+y).
(Ⅰ)求证:函数f(x)是奇函数;
(Ⅱ)如果当x∈(﹣1,0]时,有f(x)<0,试判断f(x)在(﹣1,1)上的单调性,并用定义证明你的判断;
(Ⅲ)在(Ⅱ)的条件下,若a﹣8x+1>0对满足不等式f(x﹣ ![]() )+f(
)+f( ![]() ﹣2x)<0的任意x恒成立,求a的取值范围.
﹣2x)<0的任意x恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,第一年投入资金1000万元,出售产品收入40万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80万元,同时,当预计投入的资金低于20万元时,就按20万元投入,且当年出售产品收入与上一年相等.
(1)求第![]() 年的预计投入资金与出售产品的收入;
年的预计投入资金与出售产品的收入;
(2)预计从哪一年起该公司开始盈利?(注:盈利是指总收入大于总投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为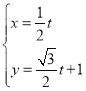 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=7,b=14,A=30°
B.a=20,b=26,A=150°
C.a=30,b=40,A=30°
D.a=72,b=60,A=135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com