
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,PA=AB=1,![]()

(1)证明:BD⊥平面PAC;
(2)若E是PC的中点,F是棱PD上一点,且BE∥平面ACF,求二面角F﹣AC﹣D的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)根据![]() ,利用勾股定理得PA⊥AB,PA⊥AD,利用线面垂直的判定定理得到PA⊥平面ABCD,从而PA⊥BD,再根据ABCD为正方形,有AC⊥BD得证.
,利用勾股定理得PA⊥AB,PA⊥AD,利用线面垂直的判定定理得到PA⊥平面ABCD,从而PA⊥BD,再根据ABCD为正方形,有AC⊥BD得证.
(2)连接ED,取ED的中点M,由三角形的中位线定理得BE∥OM,从而BE∥平面ACM,平面ACM与PD的交点即为F.然后建立空间直角坐标系,分别求得平面ACF,平面ACD的法向量,代入向量夹角公式求解.
(1)证明:∵![]() ,
,
∴PA⊥AB,PA⊥AD,AB∩AD=A,
∴PA⊥平面ABCD,
∴PA⊥BD.
又∵ABCD为正方形,∴AC⊥BD,PA∩AC=A,
∴BD⊥平面PAC.
(2)如图,
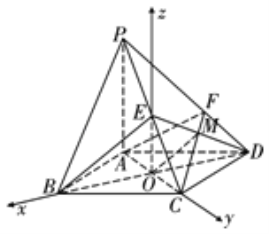
连接ED,取ED的中点M,
设AC∩BD=O,连接OM,则BE∥OM,
从而BE∥平面ACM,平面ACM与PD的交点即为F.
建立如图所示的空间直角坐标系O﹣xyz,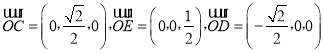 ,
,
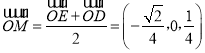 ,
,
平面ACF即平面ACM,设其法向量为![]() ,
,
则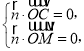 即
即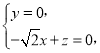 令x=1,得
令x=1,得![]() ,
,
易知平面ACD的一个法向量为![]() ,
,
∴![]() ,
,
因为二面角F﹣AC﹣D为锐二面角,
故所求余弦值为:![]() .
.


科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户,得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图,如图.
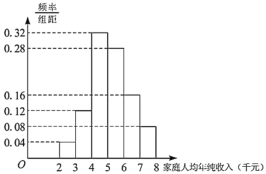
注:在频率分布直方图中,同一组数据用该区间的中点值作代表.
(1)估计该地区尚未实现小康的家庭2018年家庭人均年纯收入的平均值;
(2)2019年7月,为估计该地能否在2020年全面实现小康,收集了当地最贫困的一户家庭2019年1至6月的人均月纯收入的数据,作出散点图如下.
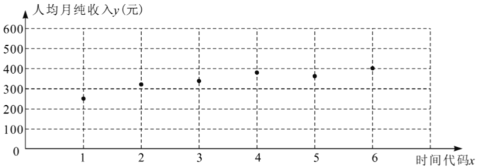
根据相关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推).试预测该家庭能否在2020年实现小康生活.
,…,依此类推).试预测该家庭能否在2020年实现小康生活.
参考数据:![]() ,
,![]() .
.
参考公式:线性回归方程![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年至201 9年我国二氧化硫的年排放量(单位:万吨)如下表,则以下结论中错误的是( )
![]()
A.二氧化硫排放量逐年下降
B.2018年二氧化硫减排效果最为显著
C.2017年至2018年二氧化硫减排量比2013年至2016年二氧化硫减排量的总和大
D.2019年二氧化硫减排量比2018年二氧化硫减排量有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的两条相邻对称轴间的距离为
的两条相邻对称轴间的距离为![]() ,把f(x)的图象向右平移
,把f(x)的图象向右平移![]() 个单位得到函数g(x)的图象,且g(x)为偶函数,则f(x)的单调递增区间为( )
个单位得到函数g(x)的图象,且g(x)为偶函数,则f(x)的单调递增区间为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.
(1)求选出的4名选手中恰好有一名女教师的选派方法数;
(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式,某市通过随机询问100名居民(男女居民各50名)喜欢支付宝支付还是微信支付,得到如下的![]() 列联表:
列联表:
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式: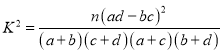 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是( )
A.有![]() 以上的把握认为“支付方式与性别有关”
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
C.在犯错误的概率不超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
D.有![]() 以上的把握认为“支付方式与性别无关”
以上的把握认为“支付方式与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() ,
,![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,已知点
两点,已知点![]() ,直线
,直线![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 是否在定直线上,若存在,求出该直线方程;若不是,说明理由.
是否在定直线上,若存在,求出该直线方程;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com