【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式，某市通过随机询问100名居民（男女居民各50名）喜欢支付宝支付还是微信支付，得到如下的
列联表：
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式：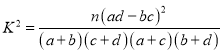
，
.
P（ | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是（ ）
A.有
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过
的前提下，认为“支付方式与性别有关”
C.在犯错误的概率不超过的前提下，认为“支付方式与性别有关”
D.有
以上的把握认为“支付方式与性别无关”
小学生10分钟口算测试100分系列答案科目：高中数学 来源： 题型：
【题目】选修4—4：坐标系与参数方程
平面直角坐标系xOy中，曲线C：
．直线l经过点P（m，0），且倾斜角为
．O为极点，以x轴正半轴为极轴，建立极坐标系．
（Ⅰ）写出曲线C的极坐标方程与直线l的参数方程；
（Ⅱ）若直线l与曲线C相交于A，B两点，且｜PA｜·｜PB｜＝1，求实数m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，PA＝AB＝1，
（1）证明：BD⊥平面PAC；
（2）若E是PC的中点，F是棱PD上一点，且BE∥平面ACF，求二面角F﹣AC﹣D的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线Γ：y2＝2px（p＞0）的焦点为F，P是抛物线Γ上一点，且在第一象限，满足
（2，2
）
（1）求抛物线Γ的方程；
（2）已知经过点A（3，﹣2）的直线交抛物线Γ于M，N两点，经过定点B（3，﹣6）和M的直线与抛物线Γ交于另一点L，问直线NL是否恒过定点，如果过定点，求出该定点，否则说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
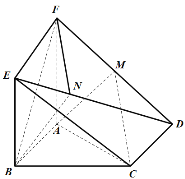
【题目】如图所示的几何体中，
平面
，
，四边形为菱形，
，点
，
分别在棱
，
上.
（1）若
平面
，设
，求
的值；
（2）若
，
，直线
与平面所成角的正切值为
，求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若函数
在
上是减函数，求实数
的取值范围；
（2）令
，是否存在实数，使得当
时，函数
的最小值是3？若存在，求出实数的值；若不存在，说明理由；
（3）当时，证明
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左右焦点分别为
，
，点
是椭圆
上一点，以
为直径的圆
：
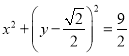过点.
（1）求椭圆的方程；
（2）过点且斜率大于0的直线
与的另一个交点为
，与直线
的交点为
，过点
且与垂直的直线
与直线交于点
，求
面积的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
是抛物线
的准线上一点，F为抛物线的焦点，P为抛物线上的点，且
，若双曲线C中心在原点，F是它的一个焦点，且过P点，当m取最小值时，双曲线C的离心率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
