[题目]已知椭圆的左右焦点分别为..点是椭圆上一点.以为直径的圆:过点.(1)求椭圆的方程,(2)过点且斜率大于0的直线与的另一个交点为.与直线的交点为.过点且与垂直的直线与直线交于点.求面积的最小值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

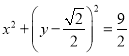【题目】已知椭圆的左右焦点分别为，，点是椭圆上一点，以为直径的圆：过点.

（1）求椭圆的方程；

（2）过点且斜率大于0的直线与的另一个交点为，与直线的交点为，过点且与垂直的直线与直线交于点，求面积的最小值.

【答案】（1）；（2）.

【解析】

(1)先求出点的坐标，再利用椭圆的定义求出的值，即得椭圆方程；

(2)设,，将直线的方程代入椭圆方程求出，进而表示出的面积，再利用基本不等式求出最小值.

解：(1)在圆的方程中，令，得到：，

所以，，

又因为且，所以点坐标为，

所以，则，，

因此椭圆的方程为；

(2)设直线：，

所以点的坐标为，

设，，将直线代入椭圆方程得：

，

所以，所以，

直线的方程为，所以点坐标为，

所以

，

当且仅当，即时取等号，

综上，面积的最小值.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】2013年至201 9年我国二氧化硫的年排放量（单位：万吨）如下表，则以下结论中错误的是（）

A.二氧化硫排放量逐年下降

B.2018年二氧化硫减排效果最为显著

C.2017年至2018年二氧化硫减排量比2013年至2016年二氧化硫减排量的总和大

D.2019年二氧化硫减排量比2018年二氧化硫减排量有所增加

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式，某市通过随机询问100名居民（男女居民各50名）喜欢支付宝支付还是微信支付，得到如下的列联表：

	支付宝支付	微信支付
男	40	10
女	25	25

附表及公式：，.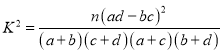

P（）	0.050	0.010	0.001
k	3.841	6.635	10.828

则下面结论正确的是（）

A.有以上的把握认为“支付方式与性别有关”

B.在犯错误的概率超过的前提下，认为“支付方式与性别有关”

C.在犯错误的概率不超过的前提下，认为“支付方式与性别有关”

D.有以上的把握认为“支付方式与性别无关”

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知在中，两直角边，的长分别为和，以的中点为原点，所在直线为轴，以的垂直平分线为轴建立平面直角坐标系，椭圆以，为焦点，且经过点.

（1）求椭圆的方程；

（2）直线：与相交于，两点，在轴上是否存在点，使得为等边三角形，若存在，求出直线的方程；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）若曲线在点处的切线与直线垂直，求函数的单调区间；

（2）若对于任意都有成立，试求的取值范围；

（3）记.当时，函数在区间上有两个零点，求实数的取值范围。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知动圆过定点，且与直线相切，动圆圆心的轨迹为，过作斜率为的直线与交于两点，过分别作的切线，两切线的交点为，直线与交于两点．

（1）证明：点始终在直线上且；

（2）求四边形的面积的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆,定点 ,为平面内一动点，以线段为直径的圆内切于圆，设动点的轨迹为曲线

（1）求曲线的方程

（2）过点的直线与交于两点，已知点，直线分别与直线交于两点，线段的中点是否在定直线上，若存在，求出该直线方程；若不是，说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义在上的函数满足: , .若方程有5个实根,则正数a的取值范围是（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】这次新冠肺炎疫情，是新中国成立以来在我国发生的传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件.中华民族历史上经历过很多磨难，但从来没有被压垮过，而是愈挫愈勇，不断在磨难中成长，从磨难中奋起.在这次疫情中，全国人民展现出既有责任担当之勇、又有科学防控之智.某校高三学生也展开了对这次疫情的研究，一名同学在数据统计中发现，从2020年2月1日至2月7日期间，日期和全国累计报告确诊病例数量（单位：万人）之间的关系如下表：