【题目】已知点
是抛物线
的准线上一点，F为抛物线的焦点，P为抛物线上的点，且
，若双曲线C中心在原点，F是它的一个焦点，且过P点，当m取最小值时，双曲线C的离心率为______.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式，某市通过随机询问100名居民（男女居民各50名）喜欢支付宝支付还是微信支付，得到如下的
列联表：
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式：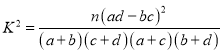
，
.
P（ | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是（ ）
A.有
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过
的前提下，认为“支付方式与性别有关”
C.在犯错误的概率不超过的前提下，认为“支付方式与性别有关”
D.有
以上的把握认为“支付方式与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
,定点
,
为平面内一动点，以线段
为直径的圆内切于圆
，设动点的轨迹为曲线
（1）求曲线的方程
（2）过点
的直线
与交于
两点，已知点
，直线
分别与直线
交于
两点，线段
的中点
是否在定直线上，若存在，求出该直线方程；若不是，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xoy中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
，过点
的直线l的参数方程为
（为参数），直线l与曲线C交于M、N两点。
（1）写出直线l的普通方程和曲线C的直角坐标方程：
（2）若
成等比数列，求a的值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，旨在积极发展我国与沿线国家经济合作关系，共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来，“一带一路”建设成果显著.如图是2015—2019年，我国对“一带一路”沿线国家进出口情况统计图，下列描述错误的是( )
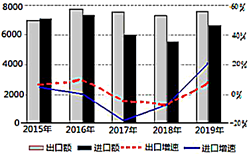
A.这五年，出口总额之和比进口总额之和大
B.这五年，2015年出口额最少
C.这五年，2019年进口增速最快
D.这五年，出口增速前四年逐年下降
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（多选题）下列说法中，正确的命题是（ ）
A.已知随机变量
服从正态分布
，
，则
．
B.以模型
去拟合一组数据时，为了求出回归方程，设
，将其变换后得到线性方程
，则
，
的值分别是
和0.3．
C.已知两个变量具有线性相关关系，其回归直线方程为
，若
，
，
，则
．
D.若样本数据
，
，…，
的方差为2，则数据
，
，…，
的方差为16．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】这次新冠肺炎疫情，是新中国成立以来在我国发生的传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件.中华民族历史上经历过很多磨难，但从来没有被压垮过，而是愈挫愈勇，不断在磨难中成长，从磨难中奋起.在这次疫情中，全国人民展现出既有责任担当之勇、又有科学防控之智.某校高三学生也展开了对这次疫情的研究，一名同学在数据统计中发现，从2020年2月1日至2月7日期间，日期
和全国累计报告确诊病例数量
（单位：万人）之间的关系如下表：
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
全国累计报告确诊病例数量 | 1.4 | 1.7 | 2.0 | 2.4 | 2.8 | 3.1 | 3.5 |
（1）根据表中的数据，运用相关系数进行分析说明，是否可以用线性回归模型拟合与的关系？
（2）求出关于的线性回归方程
（系数精确到0.01）.并预测2月10日全国累计报告确诊病例数.
参考数据：
，
，
，
.
参考公式：相关系数
回归方程
中斜率和截距的最小二乘估计公式分别为：
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
