
 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数 的一个“姊妹点对”。点对(A,B)与(B,A)可看作是同一个“姊妹点对”,已知函数
的一个“姊妹点对”。点对(A,B)与(B,A)可看作是同一个“姊妹点对”,已知函数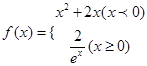 ,则
,则 的“姊妹点对”有( )
的“姊妹点对”有( ) 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源:不详 题型:解答题
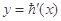 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)
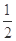 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
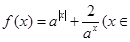 R,
R,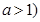 ,
,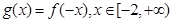 ,若
,若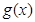 的最小值与
的最小值与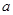 无关,求
无关,求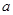 的取值范围;
的取值范围;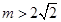 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于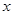 的方程
的方程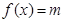 的解集
的解集查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
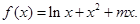
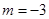 时,求函数
时,求函数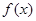 的极值;
的极值;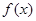 在定义域内为增函数,求实数m的取值范围;
在定义域内为增函数,求实数m的取值范围;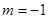 ,
,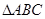 的三个顶点
的三个顶点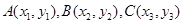 在函数
在函数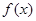 的图象上,且
的图象上,且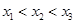 ,
,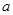 、
、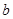 、
、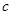 分别为
分别为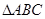 的内角A、B、C所对的边。求证:
的内角A、B、C所对的边。求证: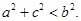
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
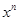 +
+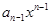 +
+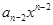 +…+
+…+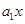 +
+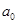 (n>2且n∈N﹡)设
(n>2且n∈N﹡)设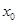 是函数f(x)的零点的最大值,则下述论断一定错误的是( )
是函数f(x)的零点的最大值,则下述论断一定错误的是( )A.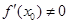 | B.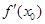 =0 =0 | C.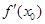 >0 >0 | D.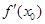 <0 <0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com