
【题目】已知函数 ,若方程
,若方程![]() 恰有
恰有![]() 个互异的实数根,则实数
个互异的实数根,则实数![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】若关于x的方程f(x)=m|x|=0恰好有4个解,
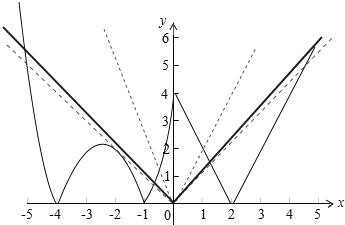
即函数y=f(x)与y=m|x|的图象有四个交点,
①当m<0时,函数y=f(x)与y=m|x|的图象无交点,不满足条件;
②当m=0时,函数y=f(x)与y=m|x|的图象有三个交点,不满足条件;
③当m>0时,若与y=mx与y=2x﹣4平行,即m=2,则函数y=f(x)与y=m|x|的图象有三个交点,
则m≥2时,函数y=f(x)与y=m|x|的图象有三个交点,
若y=﹣mx与y=﹣(x2+5x+4)相切,则函数y=f(x)与y=m|x|的图象有五个交点,
即x2+(5﹣m)x﹣4=0的△=(5﹣m)2﹣16=0,解得:m=1,或m=9(舍去),
即m=1时,函数y=f(x)与y=m|x|的图象有五个交点,
0<m<1时,函数y=f(x)与y=m|x|的图象有六个交点,
故当1<m<2时,函数y=f(x)与y=m|x|的图象有四个交点,
故实数m的取值范围为(1,2)


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() a=2csinA
a=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间![]() 上为增函数”的________________.
上为增函数”的________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,错误的为( ) 
A.AC⊥BD
B.AC=BD
C.AC∥截面PQMN
D.异面直线PM与BD所成的角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒.如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).

(1)若广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(2)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设矩形ABCD(AB>AD)的周长为24,把△ABC沿AC向△ADC折叠,AB折过去后交DC于点P,设AB=x,求△ADP的最大面积及相应x的值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com